In Part 1 and Part 2 of this series, we discussed the theory behind ARDL and the Bounds Test for cointegration. Here, we demonstrate just how easily everything can be done in EViews 9 or higher.
While our two previous posts in this series have been heavily theoretically motivated, here we present a step by step procedure on how to implement Part 1 and Part 2 in practice.
![]()
![]()
Notice that each graph exhibits a structural change around June 2007, marking the beginning of the US housing crisis. We have indicated its presence using a vertical red line. We will incorporate this information into our analysis by indicating the post crisis period with the dummy variable dum0708. Namely, the variable assumes a value of 1 in each of the months following June 2007. Moreover, a little background research on the Central Bank of Canada (CBC) reveals that starting January 2001, the CBC would commit to a new set of transparency and inflation targeting measures to recover from the late 90's dot-com crash as well as the disinflationary period in the earlier part of that decade. For this reason, to avoid having to analyze too many policy paradigm shifts, we will only focus on data in the period after January 2001. We can achieve everything with the following set of commands:
![]()
![]()
![]()
![]()
To verify whether the residuals from the model are serially uncorrelated, in the estimation view, proceed to View/Residual Diagnostics/Serial Correlation LM Test..., and select the number of lags. In our case, we chose 2. Here's the output.
![]()
Similarly, testing for residual homoskedasticity, in the estimation view, proceed to View/Residual Diagnostics/Heteroskedasticity Tests..., and select a type of test. In our case, we chose Breusch-Pagan-Godfrey. Here's the output.
![]()
To test for the presence of cointegration, in the estimation view, proceed to View/Coefficient Diagnostics/Long Run Form and Bounds Test. Below the table of coefficient estimates, we have two additional tables presenting the error correction $EC$ term and the $F$-Bounds test. The output is below.
![]()
In fact, we can visualize the fit of the long-run equation and the dependent variable by extracting the $EC$ term and subtracting from it the dependent variable. This can be done as follows. In the estimation view, proceed to Proc/Make Cointegrating Relationship and save the series under a name, say cointno. Since the cointegrating relationship is the $EC$ term, we would like to extract just the long-run relationship. To do this, simply subtract the series cointno from the dependent variable. In other words, make a new series $\text{LRno} = \text{BBY10Y} - \text{cointno}$. Finally, form a group with the variables BBY10Y and LRno, and plot. We have the following output.
![]()
![]()
![]()
![]()
![]()
![]()
To test for the presence of cointegration, we proceed again to the Long Run Form and Bounds Test view. We have the following output.
![]()
![]()
![]()
As usual, we first verify whether the residuals from the model are serially uncorrelated and homoskedastic. We have the following outputs.
![]()
![]()
![]()
![]()
While our two previous posts in this series have been heavily theoretically motivated, here we present a step by step procedure on how to implement Part 1 and Part 2 in practice.
- Get a feel for the nature of the data.
- Ensure all variables are integrated of order I$(d)$ with $d < 2$.
- Specify how deterministics enter the ARDL model. Choose DGP $i=1,\ldots,5$ from those outlined in Part 1 and Part2.
- Determine the appropriate lag structure of the model selected in Step 3.
- Estimate the model in Step 4 using Ordinary Least Squares (OLS).
- Ensure residuals from Step 5 are serially uncorrelated and homoskedastic.
- Perform the Bounds Test.
- Estimate speed of adjustment, if appropriate.
Working Example
The motivation for this entry is the classical term structure of interest rates (TSIR) literature. In a nutshell, the TSIR postulates that there exists a relationship linking the yields on bonds of different maturities. Formally: $$R(k,t) = \frac{1}{k}\sum_{j=1}^{k}\pmb{\text{E}}_tR(1,t+j-1) + L(k,t)$$ where $\pmb{\text{E}}_t$ is the expectation operator conditional on the information at time $t$, $R(k,t)$ is the yield to maturity at time $t$ of a $k$ period pure discount bond, and $L(k,t)$ are the premia typically accounting for risk. To see that cointegration is indeed possible, repeated applications of the trick, $R(k,t) = R(k,t-1) + \Delta R(k,t)$, where $\Delta R(k,t) = R(k,t) - R(k,t-1)$, leads to the following expression: $$R(k,t) - R(1,t) = \frac{1}{k}\sum_{i=1}^{k-1}\sum_{j=1}^{i}\pmb{\text{E}}_t \Delta R(1,t+j) + L(k,t)$$ It is now evident that if $R(k,t)$ are I$(1)$ processes, $\Delta R(1,t+j)$ must be I$(0)$ processes, and the linear combination $R(k,t) - R(1,t)$ are therefore I$(0)$ processes provided $L(k,t)$ is as well. In other words, the $k$ period yield to maturity is always cointegrated with the first period yield to maturity, with cointegrating vector $(1,-1)^\top$. In fact, a little more work shows that the principle holds for the spread between any two arbitrary times $k_1$ and $k_2$. That is, \begin{align*} R(k_2,t) - R(k_1,t) &= R(k_2,t) - R(1,t) + R(1,t) - R(k_1,t)\\ &= \frac{1}{k_2}\sum_{i=1}^{k_2-1}\sum_{j=1}^{i}\pmb{\text{E}}_t \Delta R(1,t+j) + L(k_2,t) - \frac{1}{k_1}\sum_{i=1}^{k_1-1}\sum_{j=1}^{i}\pmb{\text{E}}_t \Delta R(1,t+j) + L(k_1,t)\\ &\sim \text{I}(0) \end{align*} Now that we have established a theoretical basis for the exercise, we delve into practice with real data. In fact, we will work with Canadian maturities collected directly from the Canadian Socioeconomic Database from Statistics Canada, or CANSIM for short. In particular, we will be looking at cointegrating relationships between two types of marketable debt instruments: the yield on a Treasury Bill, which is a short-term (maturing at 1 month, 3 months, 6 months, and 1 year from date of issue) discounted security, and the yield on Benchmark Bonds, otherwise known as Treasury Notes, which are medium-term (maturing at 2 years, 5 years, 7 years, and 10 years from date of issue) securities with bi-yearly interest payouts. The workfile can be found here.Data Summary
The first step in any empirical analysis is an overview of the data itself. In particular, the subsequent analysis makes use of data on Treasury Bill yields maturing in 1,3,6, and 12 months, appropriately named TBILL; in addition to using data on Benchmark Bond yields (Treasury Notes) maturing in years 2,5, and 10, appropriately named BBY. Consider their graphs below:
Notice that each graph exhibits a structural change around June 2007, marking the beginning of the US housing crisis. We have indicated its presence using a vertical red line. We will incorporate this information into our analysis by indicating the post crisis period with the dummy variable dum0708. Namely, the variable assumes a value of 1 in each of the months following June 2007. Moreover, a little background research on the Central Bank of Canada (CBC) reveals that starting January 2001, the CBC would commit to a new set of transparency and inflation targeting measures to recover from the late 90's dot-com crash as well as the disinflationary period in the earlier part of that decade. For this reason, to avoid having to analyze too many policy paradigm shifts, we will only focus on data in the period after January 2001. We can achieve everything with the following set of commands:
'Set sample from Jan 2001 to end.
smpl Jan/2001 @last
'Create dummy for post 07/08 crisis
series dum0708 = @recode(@dateval("2007/06")<@date,1,0)
Testing Integration Orders
We begin our analysis by ensuring that no series under consideration is integrated of order 2 or higher. To do this, we run a unit root test on the first difference of each series. In this case, the standard ADF test will suffice. A particularly easy way of doing this is creating a group object with all variables of interest, and then running a unit root test on the group, specifying that the test should be done on the individual series. In the group view then, proceed to Proc/Unit Root Test..., and choose the appropriate options.
Deterministic Specifications
Selecting an appropriate model to fit the data is both art and science. Nevertheless, there are a few guidelines. Any model in which the series are not centered about zero will typically require a constant term, whereas any model in which the series exhibit a trend, will in general have better fit when a trend term is incorporated. Our discussion in Part 1 and Part 2 of this series discussed the possibility of selecting from five different DGP specifications, termed Case 1 through Case 5. In fact, we will consider several different model specifications with various variable combinations.- Model 1: The Model under consideration will look for a relationship between the 10 Year Benchmark Bond Yield and the 1 Month T-Bill. In particular, the model will restrict the constant to enter the cointegrating relationship, corresponding to the DGP and Regression Model specified in Case 2 in Part 1 and Part 2.
- Model 2: The Model under consideration will look for a relationship between the 6, 3, and 1 Month T-Bills. Here, the model will leave the constant unrestricted, corresponding to the DGP and Regression Model specified in Case 3 in Part 1 and Part 2.
- Model 3: The Model under consideration will look for a relationship between the 2 Year Benchmark Bond Yield, and the 1 Year and 1 Month T-Bills. Here, the model will again leave the constant unrestricted, corresponding to the DGP and Regression Model specified in Case 3 in Part 1 and Part 2.
Specifying ARDL Lag Structure
Selecting an appropriate number of lags for the model under consideration is again, both science and art. Unless the number of lags is specified by economic theory, the econometrician has several tools at his disposal to select lag length optimally. One possibility is to select the maximal number of lags for the dependent variable, say $p$, and the maximal number of lags for each of the regressor variables, say $q$, and then run a barrage of regressions with all the different possible combinations of lags that can be formed using this specification. In particular, if there are $k$ regressors, the maximum number of combinations of the set of numbers $\{1, \ldots p\}$ and $k$ additional sets of numbers $\{0,\ldots, q\}$, is $p\times (q + 1)^k$. For instance, with EViews default values $p = q = 4$, the total number of models under consideration would be 100. The optimal combination is then set as that which minimizes some information criterion, say Akaike (AIC), Schwarz (BIC), Hannan-Quinn (HQ), or even the adjusted $R^2$. EViews offers the user an option on how to select from among these, and we will discuss this when we explore estimation next.Estimation, Residual Diagnostics, Bounds Test, and Speed of Adjustment
ARDL models are typically estimated using standard least squares techniques. In EViews, this implies that one can estimate ARDL models manually using an equation object with the Least Squares estimation method, or resort to the built-in equation object specialized for ARDL model estimation. We will use the latter. Open the equation dialog by selection Quick/Estimate Equation or by selecting Object/New Object/Equation and then selecting ARDL from the Method dropdown menu. Proceed by specifying each of the following:- List the relevant dynamic variables in the Dynamic Specification field. This is a space delimited list where the dependent variable is followed by the regressors which will form the long-run equation. Do NOT list variables which are not part of the long-run equation, but part of the estimated model. Those variables will be specified in the Fixed Regressors field below.
- Specify whether Automatic or Fixed lag selection will be used. Note that even if Automatic lag selection is preferred, maximum lag-orders need to be specified for the dependent variable as well as the regressors. If you wish to specify how automatic selection is computed, please click on the Options tab and select the preferred information criterion under the Model selection criteria dropdown menu. Finally, note that in EViews 9, if Fixed lag selection is preferred, all regressors will have the same number of lags. EViews 10 will allow the user to fix lags specific to each regressor under consideration.
- In the Fixed Regressors field, specify all variables other than the constant and trend, which will enter the model for estimation, but will not be a part of the long-run relationship. This list can include variables such as dummies or other exogenous variables.
- In the Fixed Regressors field, specify how deterministic specifications enter the long-run relationship. This is a dropdown menu which corresponds to the 5 different DGP cases mentioned earlier, and explored in Part 1 and Part 2 of this series. In particular, the Trend Specification dropdown menu offers the following options:
- None: This corresponds to Case 1 -- the no constant and trend case.
- Rest. constant: This corresponds to Case 2 -- the restricted constant and no trend case.
- Unrest. constant: This corresponds to Case 3 -- the unrestricted constant and no trend case.
- Rest. linear trend: This corresponds to Case 4 -- the restricted linear trend and unrestricted constant case.
- Unrest. constant and trend: This corresponds to Case 5 -- the unrestricted constant and unrestricted linear trend case. Note that this case will be available starting with EViews version 10.
Model 1: No Cointegrating Relationship
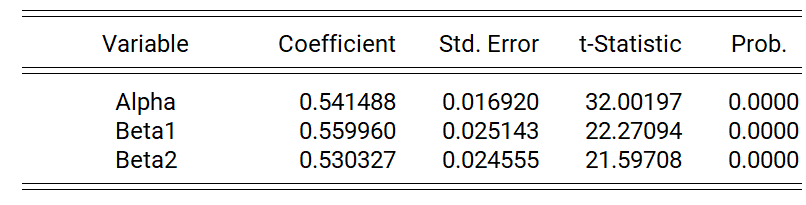
In this model, the dependent variable is the 10 Year Benchmark Bond Yield, while the dynamic regressor is the 1 Month T-Bill. Moreover, the DGP under consideration is a restricted constant, or Case 2, and we include the variable dum0708 as our non-dynamic regressor. We have the following output.
To verify whether the residuals from the model are serially uncorrelated, in the estimation view, proceed to View/Residual Diagnostics/Serial Correlation LM Test..., and select the number of lags. In our case, we chose 2. Here's the output.
Similarly, testing for residual homoskedasticity, in the estimation view, proceed to View/Residual Diagnostics/Heteroskedasticity Tests..., and select a type of test. In our case, we chose Breusch-Pagan-Godfrey. Here's the output.
To test for the presence of cointegration, in the estimation view, proceed to View/Coefficient Diagnostics/Long Run Form and Bounds Test. Below the table of coefficient estimates, we have two additional tables presenting the error correction $EC$ term and the $F$-Bounds test. The output is below.
In fact, we can visualize the fit of the long-run equation and the dependent variable by extracting the $EC$ term and subtracting from it the dependent variable. This can be done as follows. In the estimation view, proceed to Proc/Make Cointegrating Relationship and save the series under a name, say cointno. Since the cointegrating relationship is the $EC$ term, we would like to extract just the long-run relationship. To do this, simply subtract the series cointno from the dependent variable. In other words, make a new series $\text{LRno} = \text{BBY10Y} - \text{cointno}$. Finally, form a group with the variables BBY10Y and LRno, and plot. We have the following output.
Model 2: Usual Cointegrating Relationship
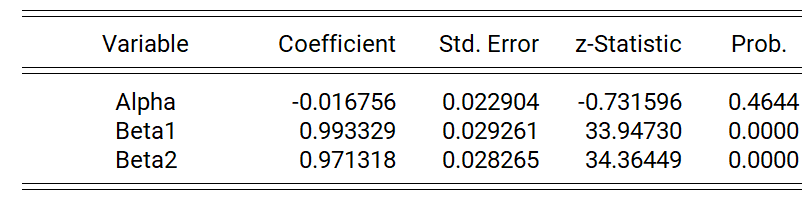
In this model, the dependent variable is the 6 Months T-Bill, while the dynamic regressors are the 3 and 1 Month T-Bills. Moreover, the DGP under consideration specifies an unrestricted constant, or Case 3, and we include the variable dum0708 as our non-dynamic regressor. To avoid repetition, we will not present the output, but skip immediately to verifying whether the residuals from the model are serially uncorrelated and homoskedastic. We have the following outputs.
To test for the presence of cointegration, we proceed again to the Long Run Form and Bounds Test view. We have the following output.
Model 3: Nonsensical Cointegrating Relationship
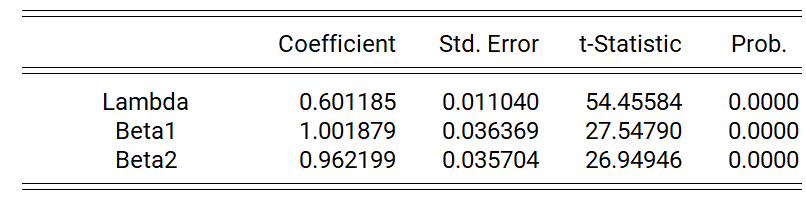
In this model, the dependent variable is the 2 Year Benchmark Bond Yield, while the dynamic regressors are the 1 Year and 1 Month T-Bills. Moreover, the DGP under consideration specifies an unrestricted constant, or Case 3, and we include the variable dum0708 as our non-dynamic regressor. To avoid repetition, we will only present tables where necessary to derive inference.As usual, we first verify whether the residuals from the model are serially uncorrelated and homoskedastic. We have the following outputs.
EViews Program and Files
We close this series with the EViews program script that will automate most of the output we have provided above. To use the script, you will need the EViews workfile: ARDL.EXAMPLE.WF1
'---------
'Preliminaries
'---------
'Open Workfile
'wfopen(type=txt) http://www5.statcan.gc.ca/cansim/results/cansim-1760043-eng-2216375457885538514.csv colhead=2 namepos=last names=(date, 'bby2y,bby5y,bby10y,tbill1m,tbill3m,tbill6m,tbill1y) skip=3
'pagecontract if @trend<244
'pagestruct @date(date)
wfuse pathto...ardl.example.WF1
'Set sample from Jan 2001 to end.
smpl Jan/2001 @last
'Create dummy for post 07/08 crisis
series dum0708 = @recode(@dateval("2007/06")<@date,1,0)
'Create Group of all Variables
group termstructure tbill1m tbill3m tbill6m tbill1y bby2y bby5y bby10y
'Graph all series
termstructure.line(m) across(@SERIES,iscale, iscalex, nodispname, label=auto, bincount=5)
'Do UR test on each series
termstructure.uroot(dif=1, adf, lagmethod=sic)
'---------
'No Relationship
'---------
'ARDL: 10y Bond Yields and 1 Month Tbills.
equation ardlno.ardl(trend=const) bby10y tbill1m @ dum0708
'Run Residual Serial Correlation Test
ardlno.auto
'Run Residual Heteroskedasticity Test
ardlno.hettest @regs
'Make EC equation.
ardlno.makecoint cointno
'Plot Dep. Var and LR Equation
group groupno bby10y (bby10y - cointno)
freeze(mode=overwrite, graphno) groupno.line
graphno.axis(l) format(suffix="%")
graphno.setelem(1) legend(BBY10Y: 10 Year Canadian Benchmark Bond Yields)
graphno.setelem(2) legend(Long run relationship (BBY10Y - COINTNO))
show graphno
'---------
'Non Degenerate Relationship
'---------
'ARDL term structure of Bond Yields. (Non-Degenerate)
equation ardlnondeg.ardl(deplags=6, reglags=6, trend=uconst, cov=hac, covlag=a, covinfosel=aic) tbill6m tbill3m tbill1m @ dum0708
'Run Residual Serial Correlation Test
ardlnondeg.auto
'Run Residual Heteroskedasticity Test
ardlnondeg.hettest @regs
'Make EC equation.
ardlnondeg.makecoint cointnondeg
'Plot Dep. Var and LR Equation
group groupnondeg tbill6m (tbill6m - cointnondeg)
groupnondeg.line
freeze(mode=overwrite, graphnondeg) groupnondeg.line
graphnondeg.axis(l) format(suffix="%")
graphnondeg.setelem(1) legend(TBILL6M: 6 Month Canadian T-Bill Yields)
graphnondeg.setelem(2) legend(Long run relationship (TBILL6M - COINTNONDEG))
show graphnondeg
'---------
'Degenerate Relationship
'---------
'ARDL term structure of Bond Yields. (Degenerate)
equation ardldeg.ardl(trend=uconst, cov=hac, covlag=a, covinfosel=aic) bby2y tbill1y tbill1m @ dum0708
'Run Residual Serial Correlation Test
ardldeg.auto
'Run Residual Heteroskedasticity Test
ardldeg.hettest @regs
'Make EC equation.
ardldeg.makecoint cointdeg
'Plot Dep. Var and LR Equation
group groupdeg bby2y (bby2y - cointdeg)
freeze(mode=overwrite, graphdeg) groupdeg.line
graphdeg.axis(l) format(suffix="%")
graphdeg.setelem(1) legend(BBY2Y: 2 Year Canadian Benchmark Bond Yields)
graphdeg.setelem(2) legend(Long run relationship (BBY2Y - COINTDEG))
show graphdeg
