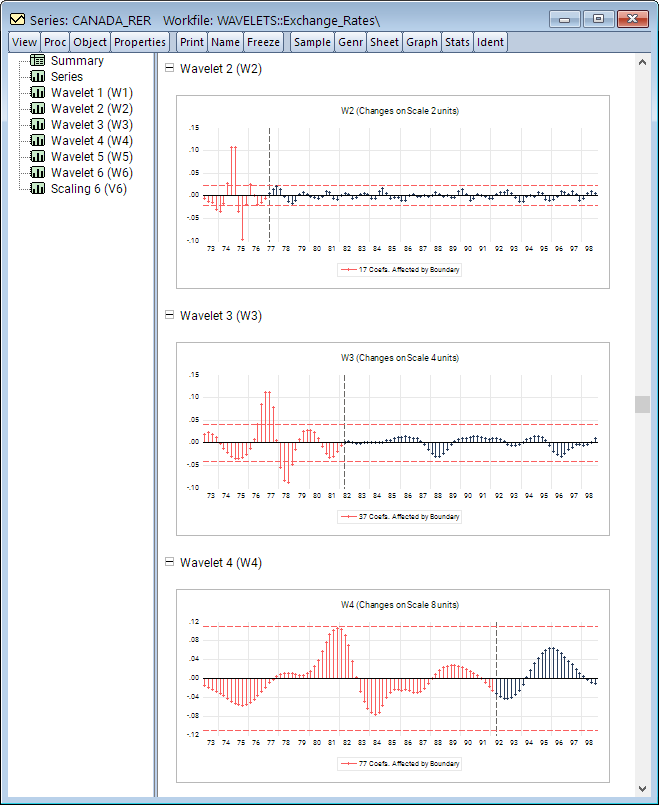
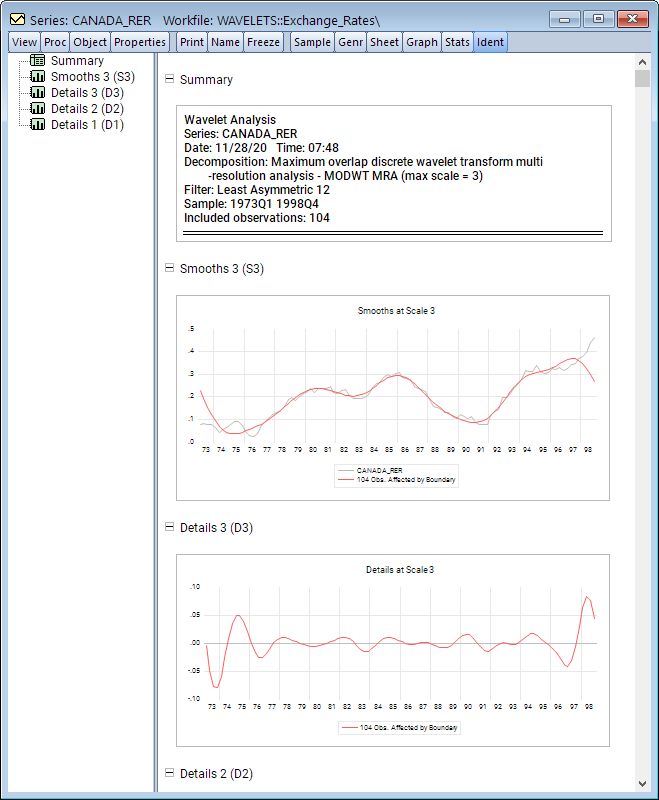
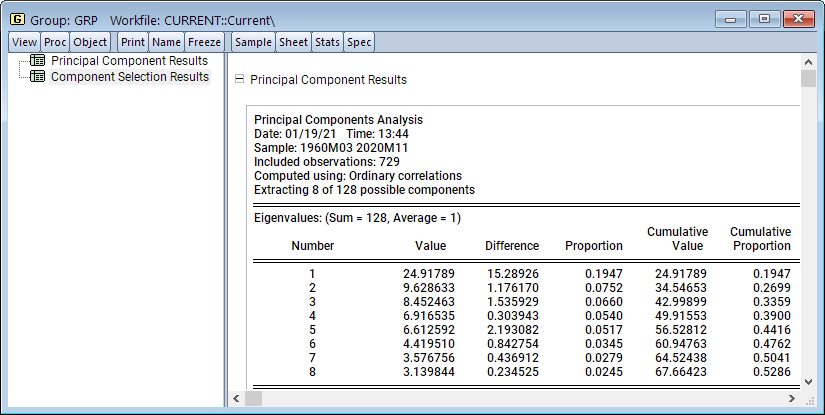
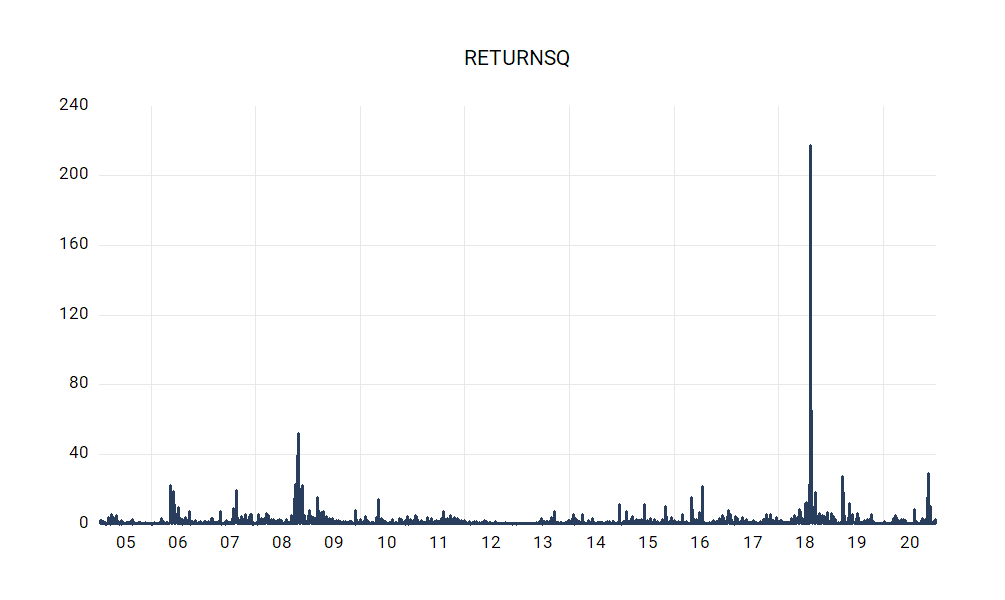
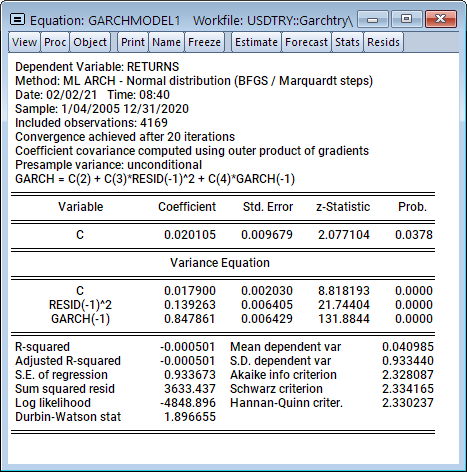
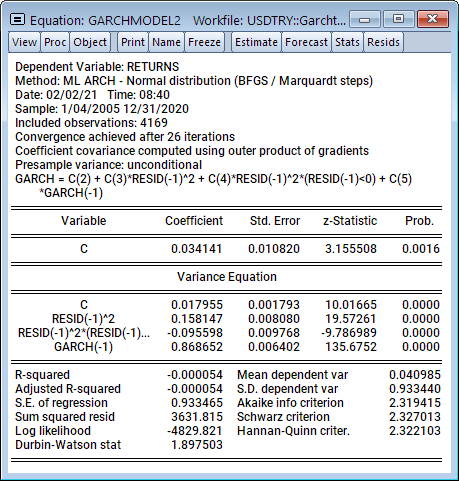
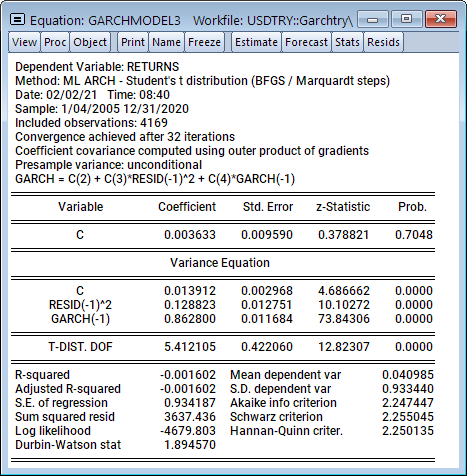
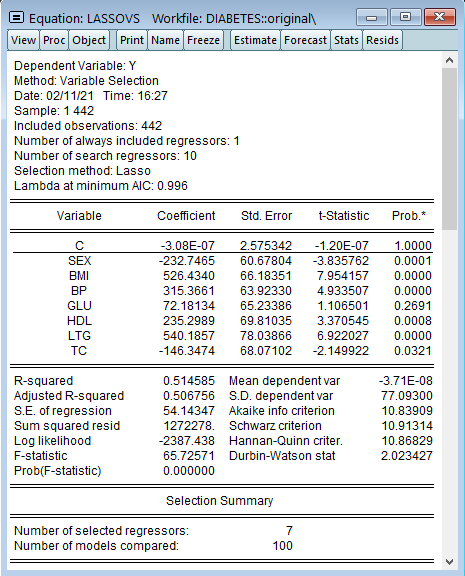
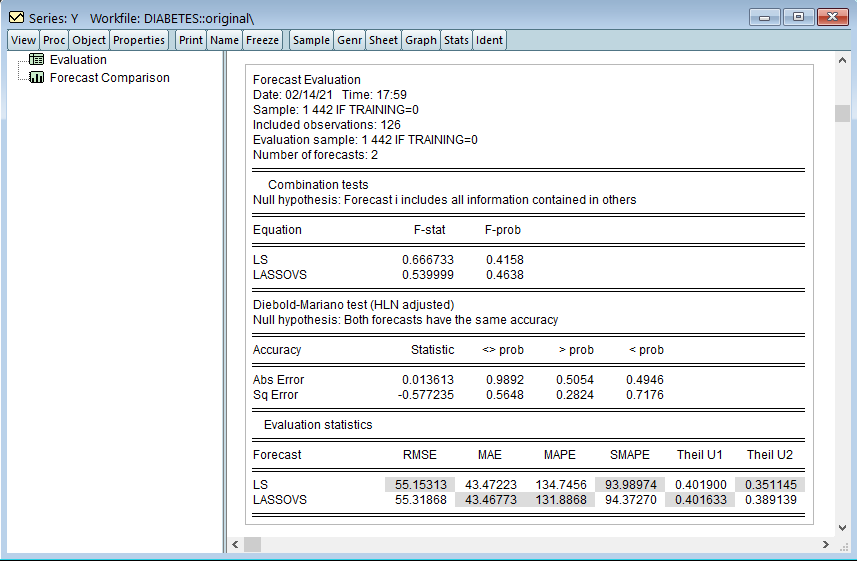
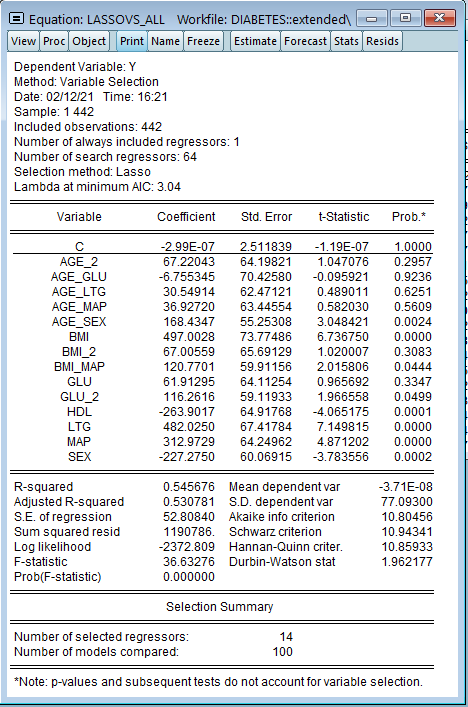
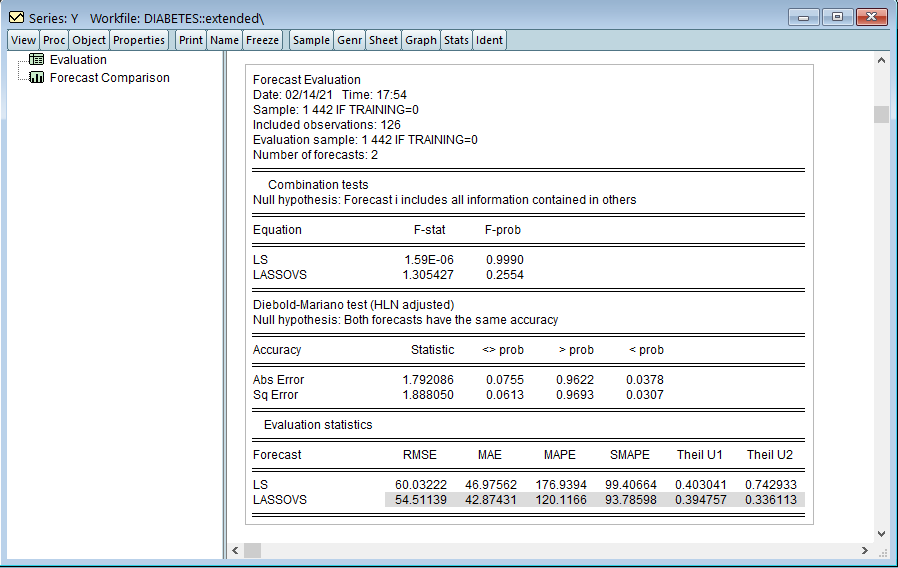
Analysis of macroeconomic time series often involves decomposing a series into a trend and cycle components. In this blog post, we describe the Kamber, Morley, and Wong (2018) Beveridge-Nelson (BN) filter and the associated EViews add-in.
Table of Contents
- Introduction
- The BN Decomposition
- The BN Filter
- Why Use the BN Filter
- BN Filter Implementation
- Conclusion
- Files
- References
Introduction
In this blog entry, we will discuss the Beveridge-Nelson (BN) filter - the Kamber, Morley, and Wong (2018) modification of the well-known Beveridge and Nelson (1981) decomposition. In particular, we will discuss the application of both procedures to estimating the output gap, which the US Bureau of Economic Analysis (BEA) and the Congressional Budget Office (CBO) define as the proportional deviation of the real actual gross domestic product (GDP) from the real potential GDP.The analysis to follow will use quarterly data from the post World War II period 1947Q1 to 2019Q3 and will be downloaded from the FRED database. In this regard, we begin by creating a new quarterly workfile as follows:
- From the main EViews window, click on File/New/Workfile....
- Under Frequency select Quarterly.
- Set the Start date to 1947Q1 and the set the End date to 2019Q3
- Hit OK.
- From the main EViews window, click on File/Open/Database....
- From the Database/File Type dropdown, select FRED Database.
- Hit OK.
- From the FRED database window, click on the Browse button.
- Next, click on All Series Search and in the Search for box,type GDPC1. (This is the real actual seasonally adjusted GDP)
- Drag the series over to the workfile to make it available for analysis.
- Again, in the Search for box, type GDPPOT. (This is the real potential seasonally unadjusted GDP estimated by the CBO)
- Drag the series over to the workfile to make it available for analysis.
- Close the FRED windows as they are no longer needed.
 |  |
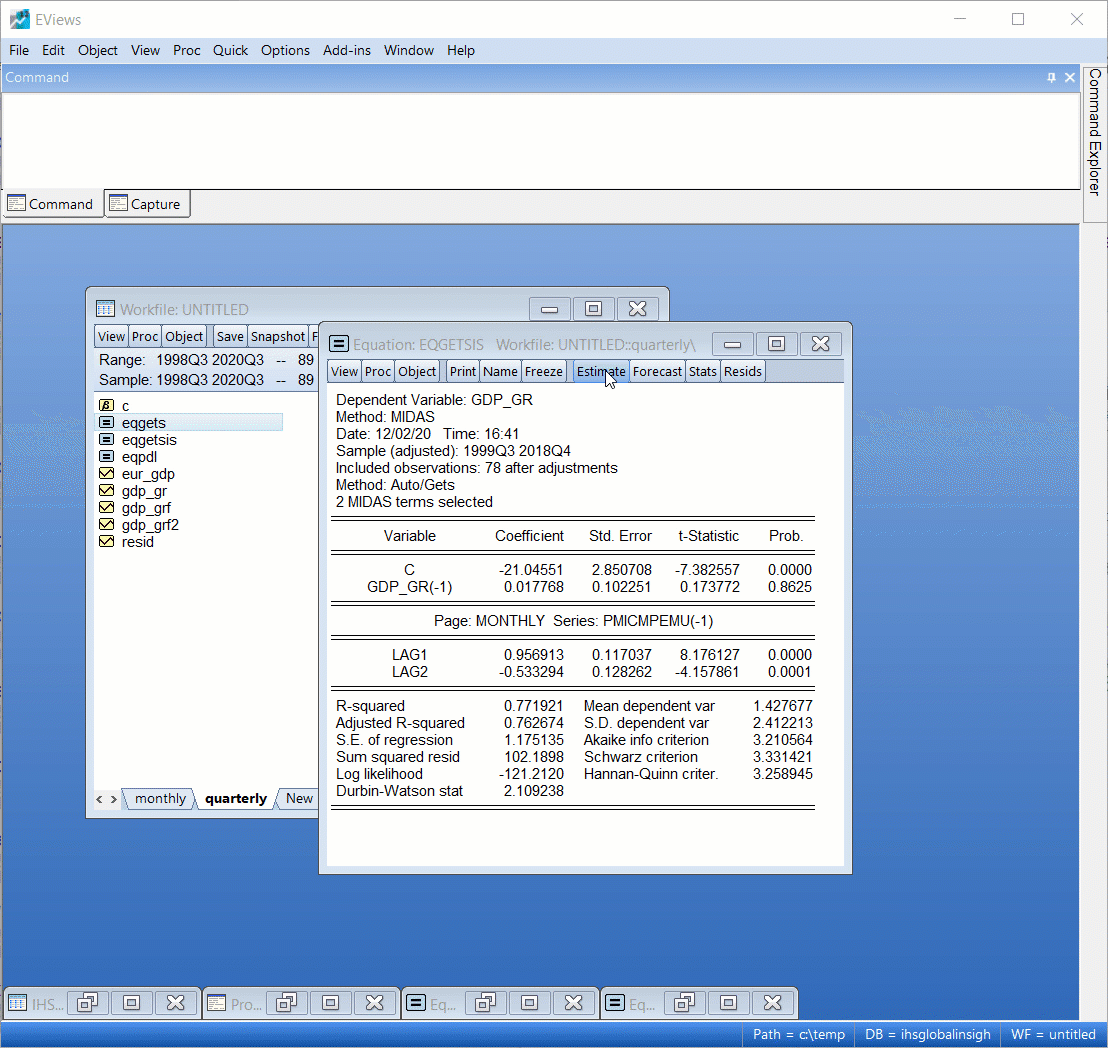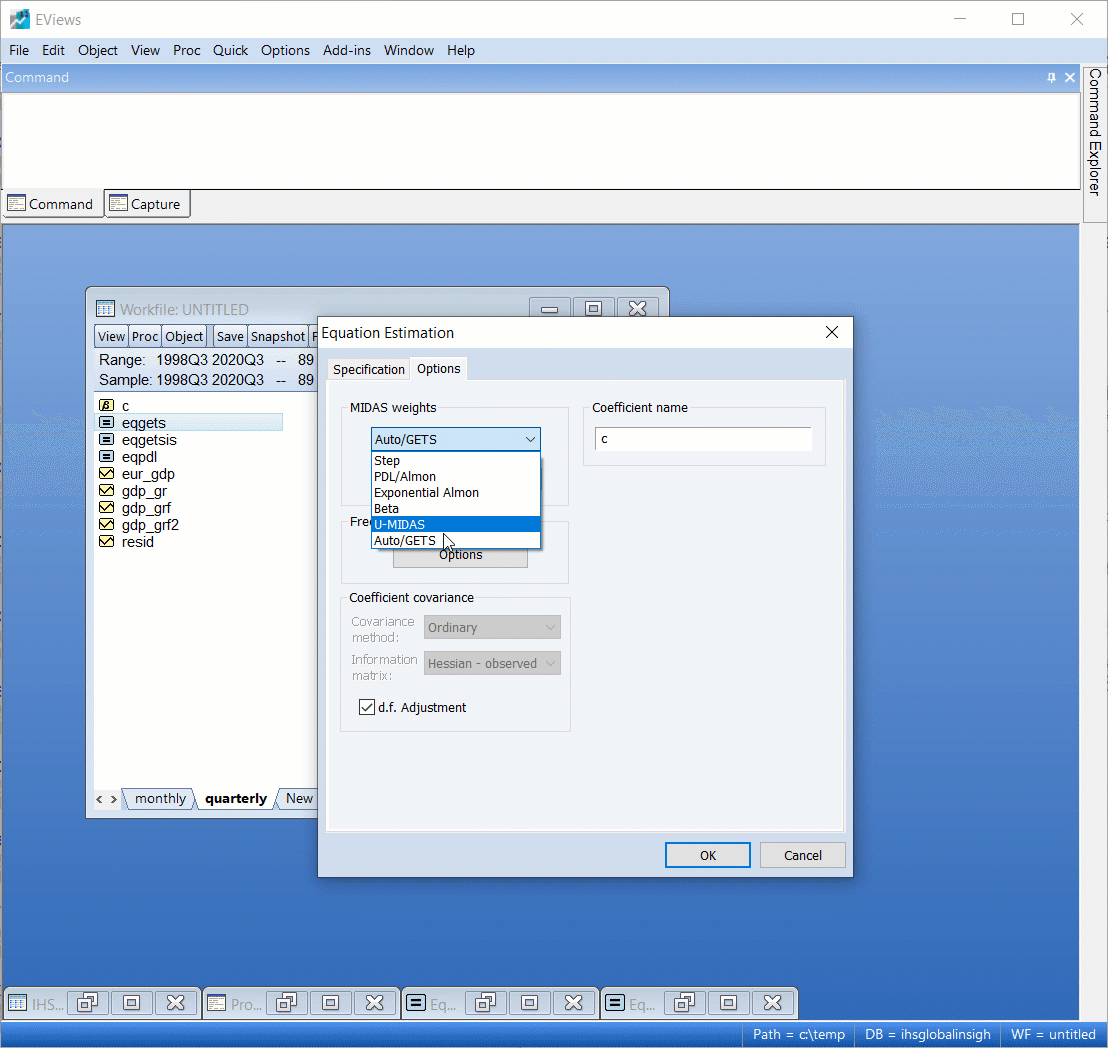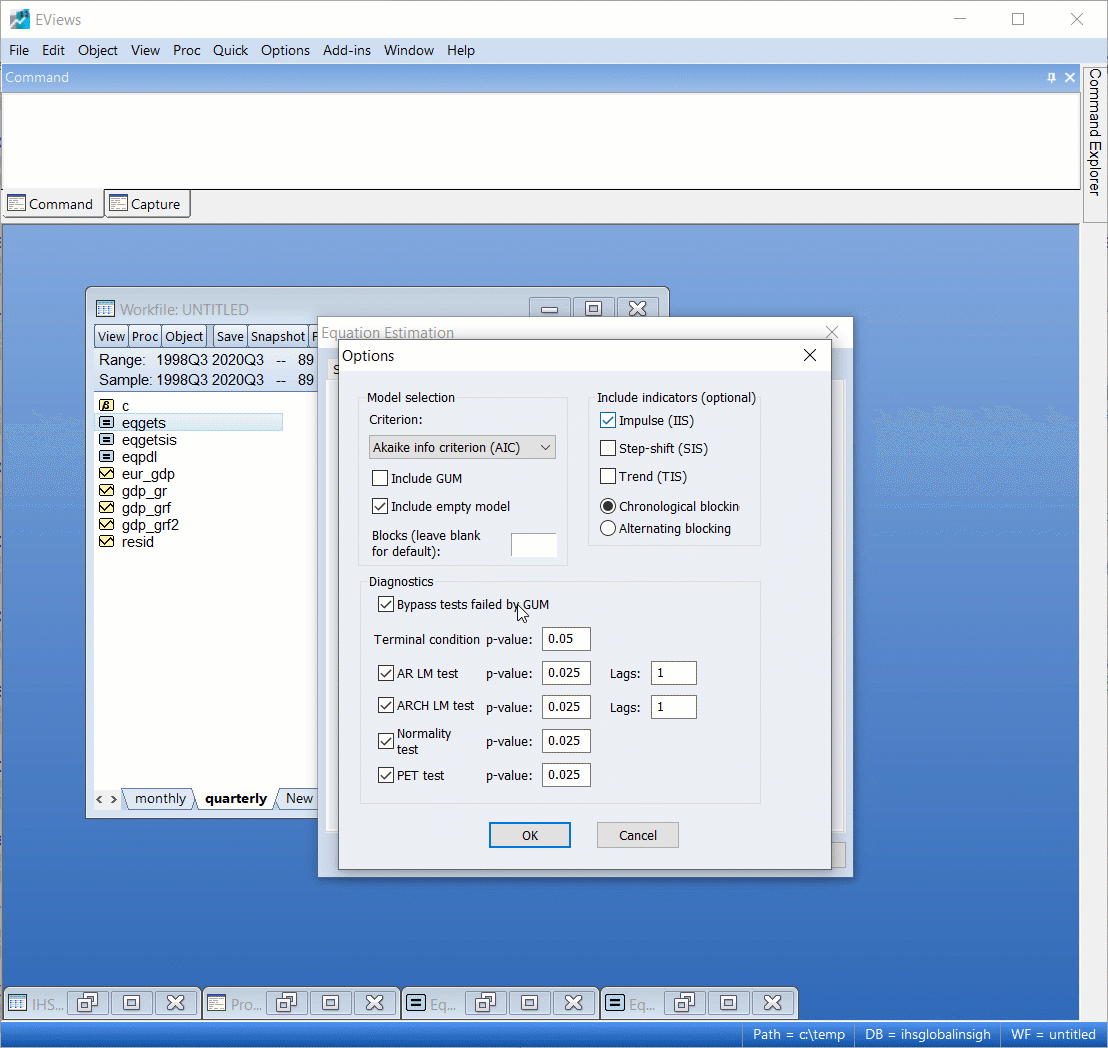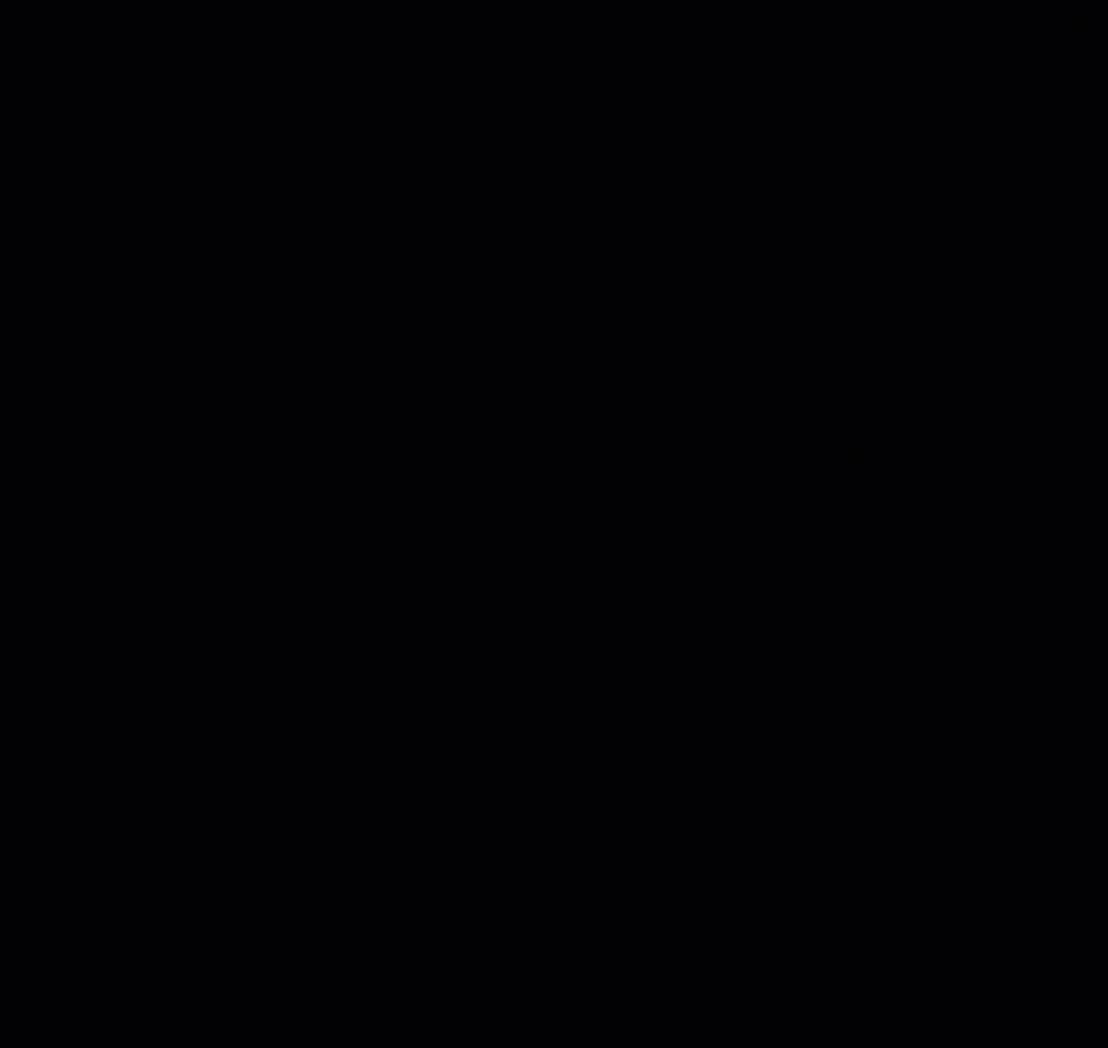
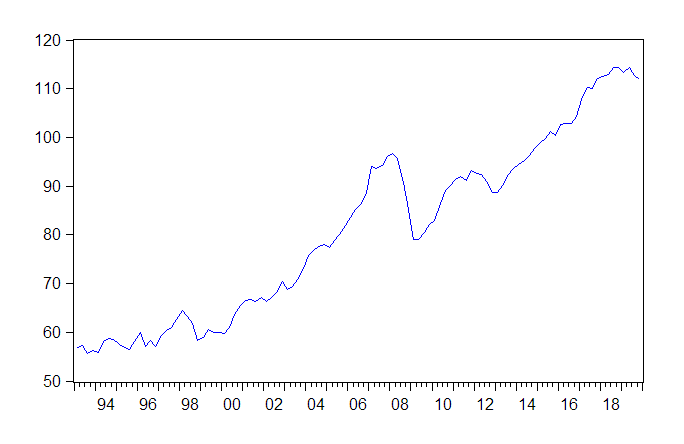
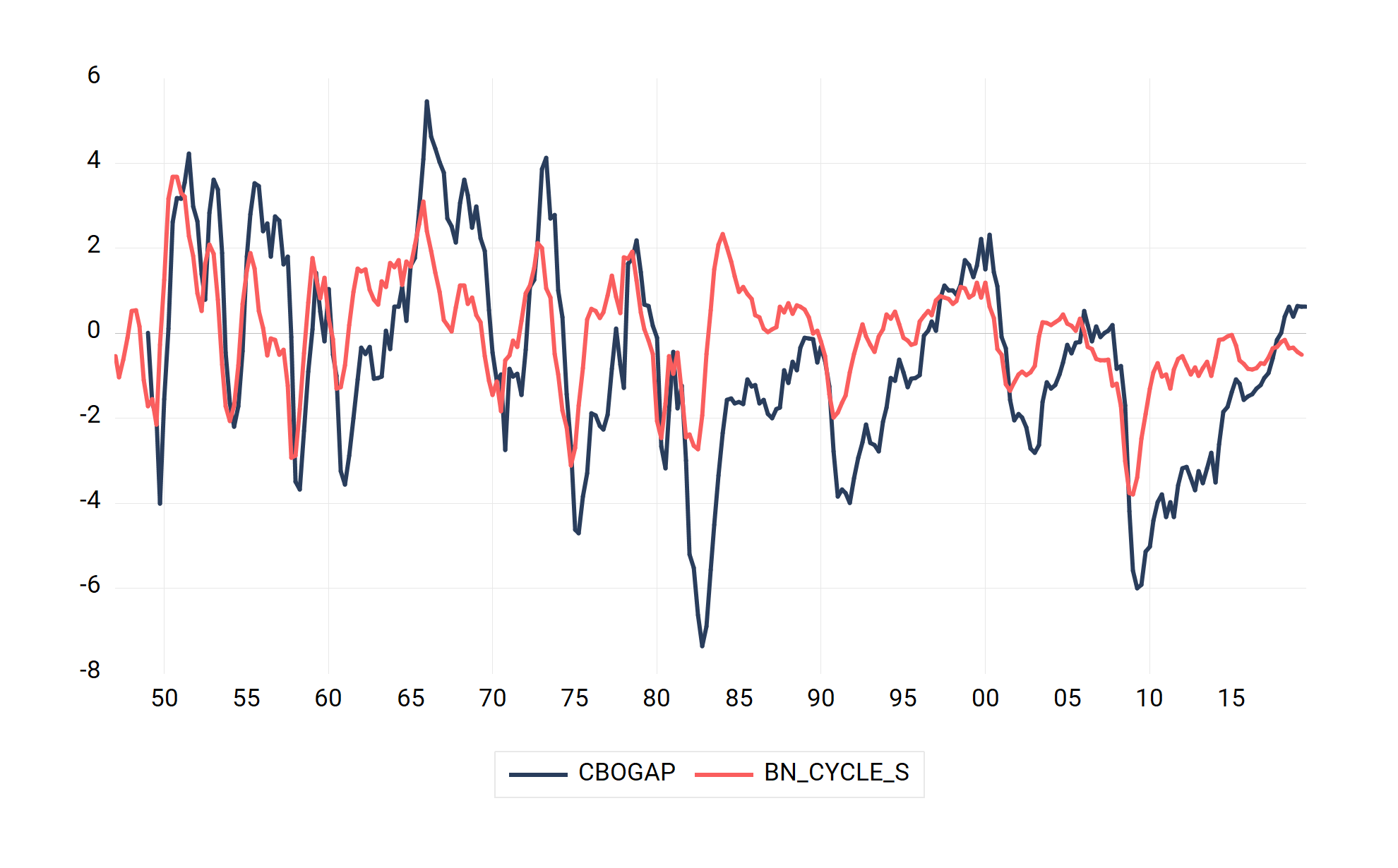
We now show how to obtain the implied estimate of the output gap from the CBO to provide the user some perspective on how to obtain the output gap. In particular, the CBO implied estimate of the output gap is defined using the formula: $$ CBOGAP = 100\left(\frac{GDP - GDPPOT}{GDPPOT}\right) $$ For reference, we will create this series in EViews and call it CBOGAP. This is done by issuing the following command:
rename gdpc1 gdp
We also plot CBOGAP below:
series cbogap = 100*(gdp-gdppot)/gdppot
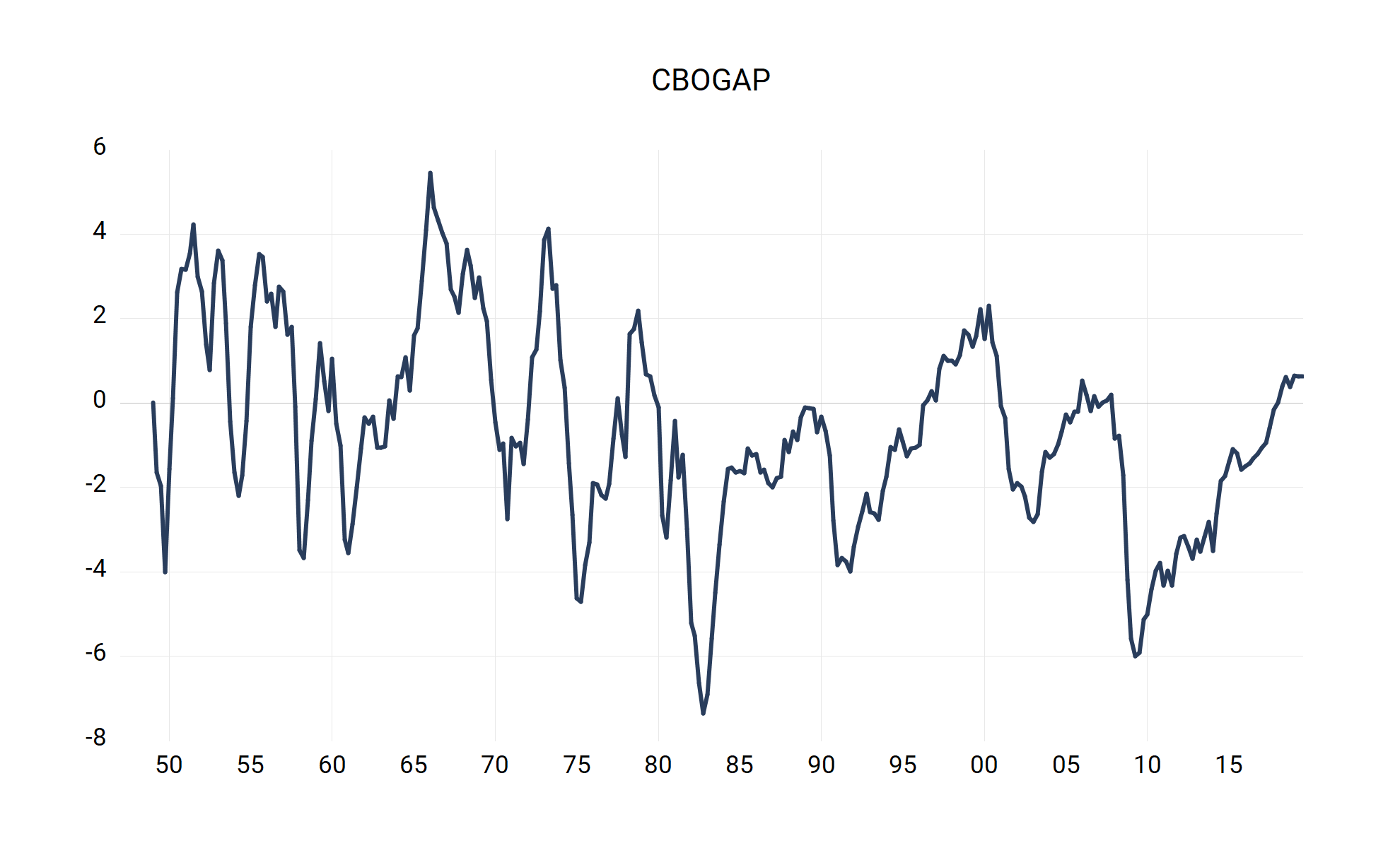 |
BN Decomposition
Recall here that for any time series $ y_{t} $, the BN decomposition determines a trend process $ \tau_{t} $ and a cycle process $ c_{t} $, such that $ y_{t} = \tau_{t} + c_{t} $. In this regard, the trend component $ \tau_{t} $ is the deviation of the long-horizon conditional forecast of $ y_{t} $ from its deterministic drift $ \mu $. In other words: $$ \tau_{t} = \lim_{h\rightarrow \infty} E_{t}\left(y_{t+h} - h\mu\right) \quad \text{where} \quad \mu = E(\Delta y_{t}) $$ On the other hand, the cyclical component is the deviation of the underlying process from its long-horizon forecast. Intuitively, when $ y_{t} $ represents the GDP of some economy, the cycle process $ c_{t} = y_{t} - \tau_{t}$ is interpreted as the output gap.In practice, in order to capture the autocovariance structure of $ \Delta y_{t} $, the BN decomposition starts by first fitting an autoregressive moving-average (ARMA) model to $ \Delta(y) $ and then proceeds to derive $ \tau_{t} $ and $ c_{t} $. For instance, when the model of choice is AR(1), the BN decomposition derives from the following steps:
- Fit an AR(1) model to $ \Delta y_{t} $: $$ \Delta y_{t} = \widehat{\alpha} + \widehat{\phi}\Delta y_{t-1} + \widehat{\epsilon}_{t} $$
- Estimate the deterministic drift as the unconditional mean process: $$ \widehat{\mu} = \frac{\widehat{\alpha}}{1 - \widehat{\phi}} $$
- Estimate the BN trend process: $$ \widehat{\tau}_{t} = \left(y_{t} + \left(\frac{\widehat{\phi}}{1 - \widehat{\phi}}\right) \Delta y_{t}\right) - \left(\frac{\widehat{\phi}}{1 - \widehat{\phi}}\right) \widehat{\mu}$$
- Estimate the BN cycle component: $$ \widehat{c}_{t} = y_{t} - \widehat{\tau}_{t} $$
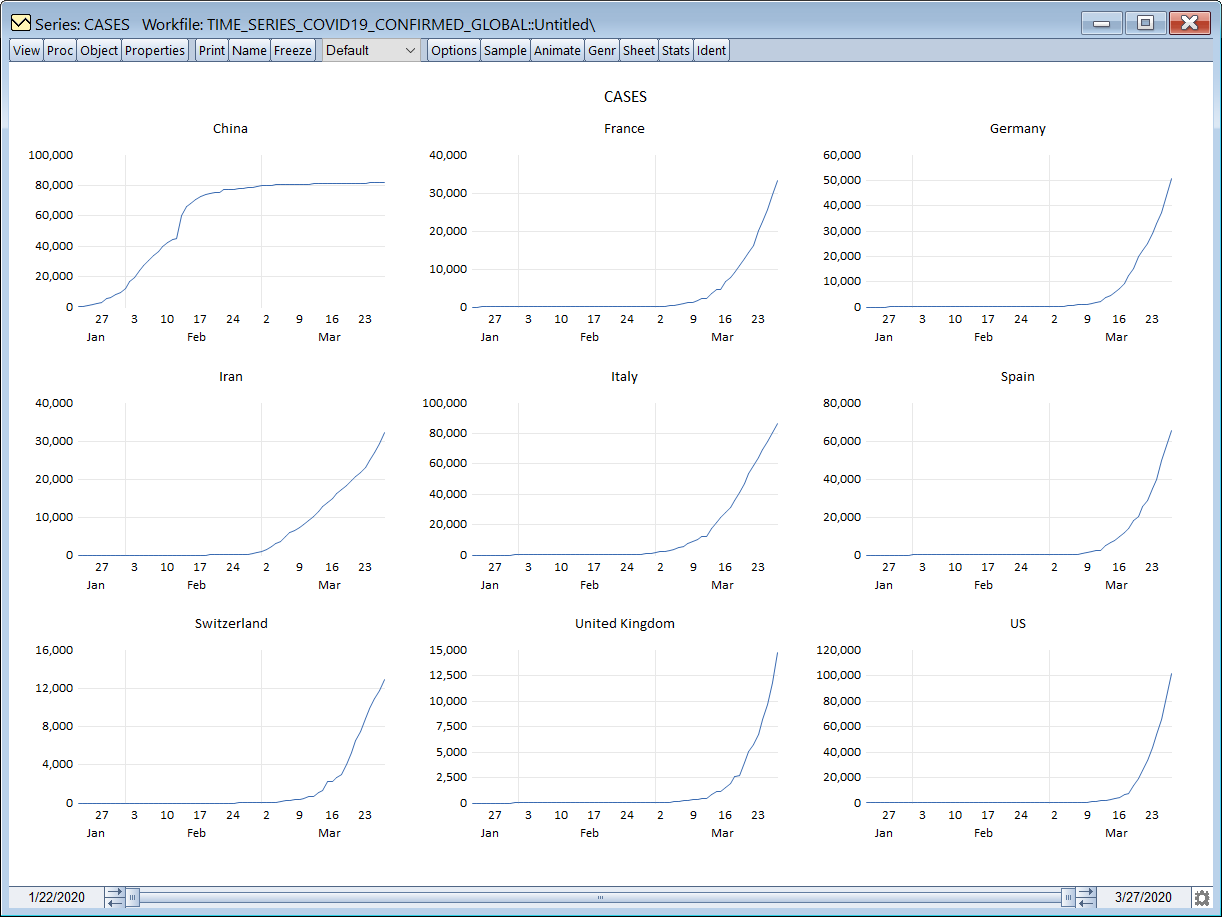
As an illustrative example, consider the BN decomposition of US quarterly real GDP. To conform with the Kamber, Morley, and Wong (2018) paper, we will also transform the raw US real GDP as 100 times its logarithm. In this regard, we generate a new EViews series object LOGGDP by issuing the following command:
At last, following the 4 steps outlined earlier, we derive the BN decomposition in EViews as follows:
series loggdp = 100 * log(gdp)
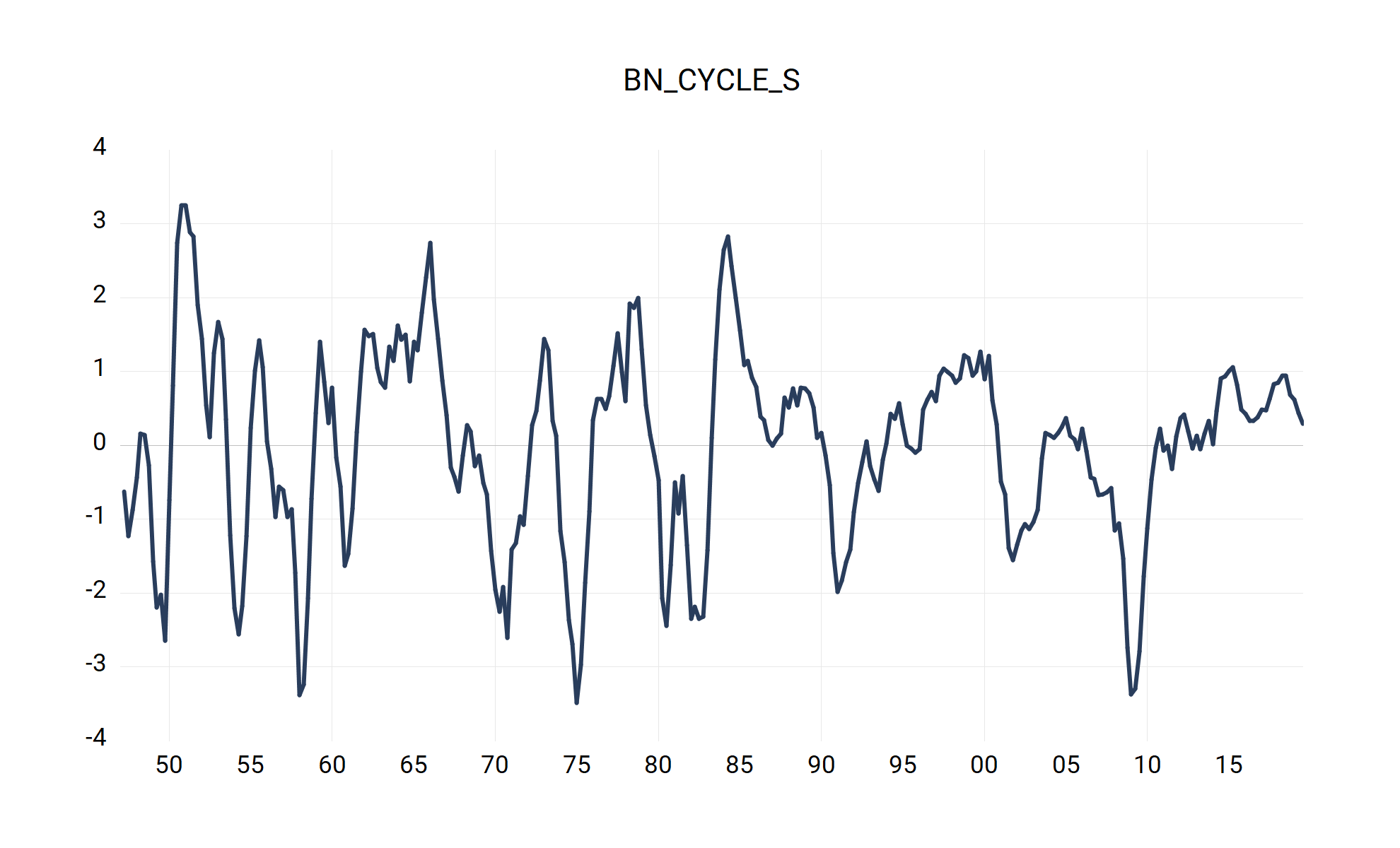
The BN trend and cycle series are displayed in Figure 2 below.
series dy = d(loggdp)
equation ar1.ls dy c dy(-1) 'Step 1
scalar mu = c(1)/(1-c(2)) 'Step 2
series bntrend = loggdp + (dy - mu)*c(2)/(1 - c(2)) 'Step 3
series bncycle = loggdp - bntrend 'Step 4
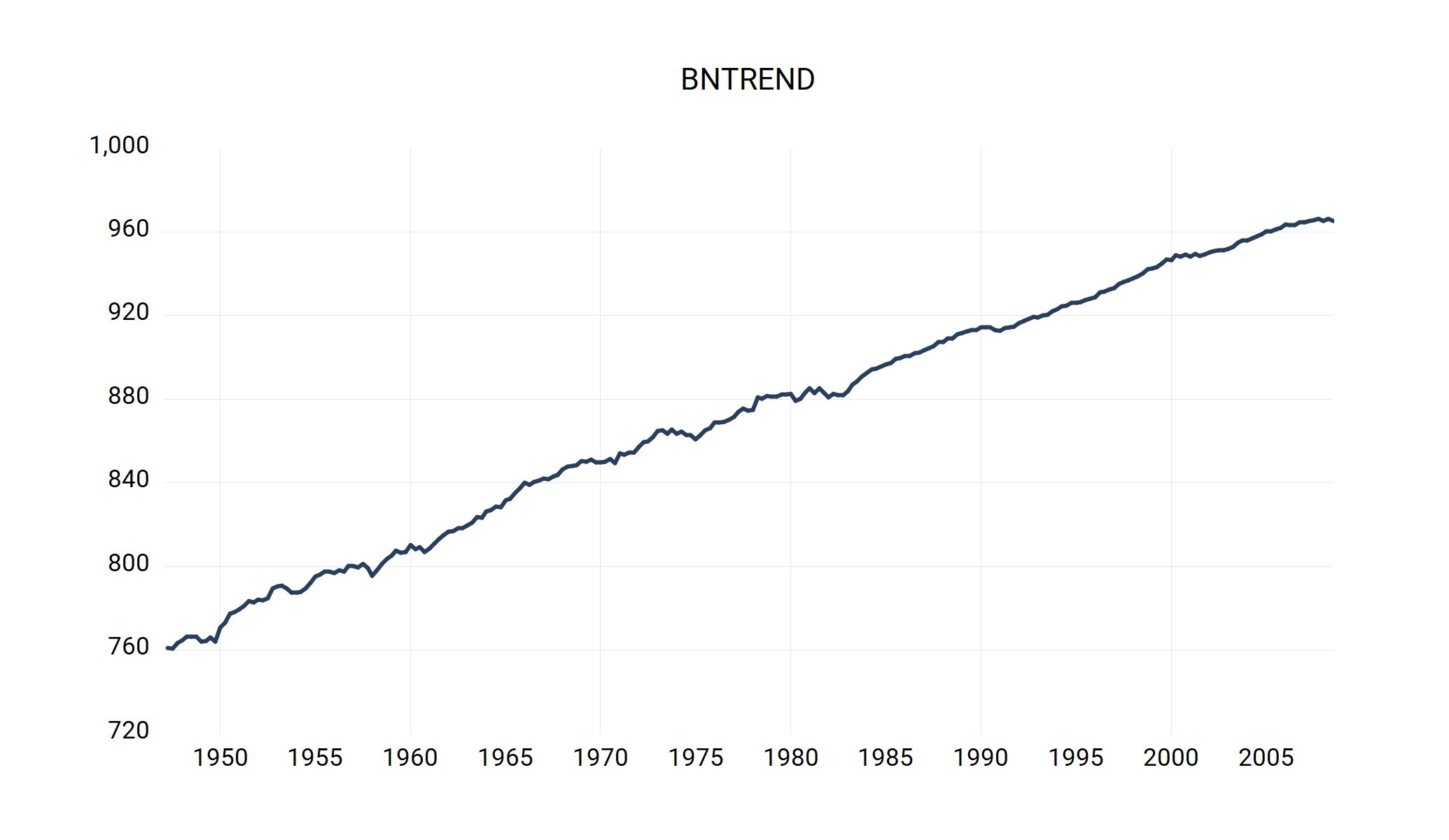 | 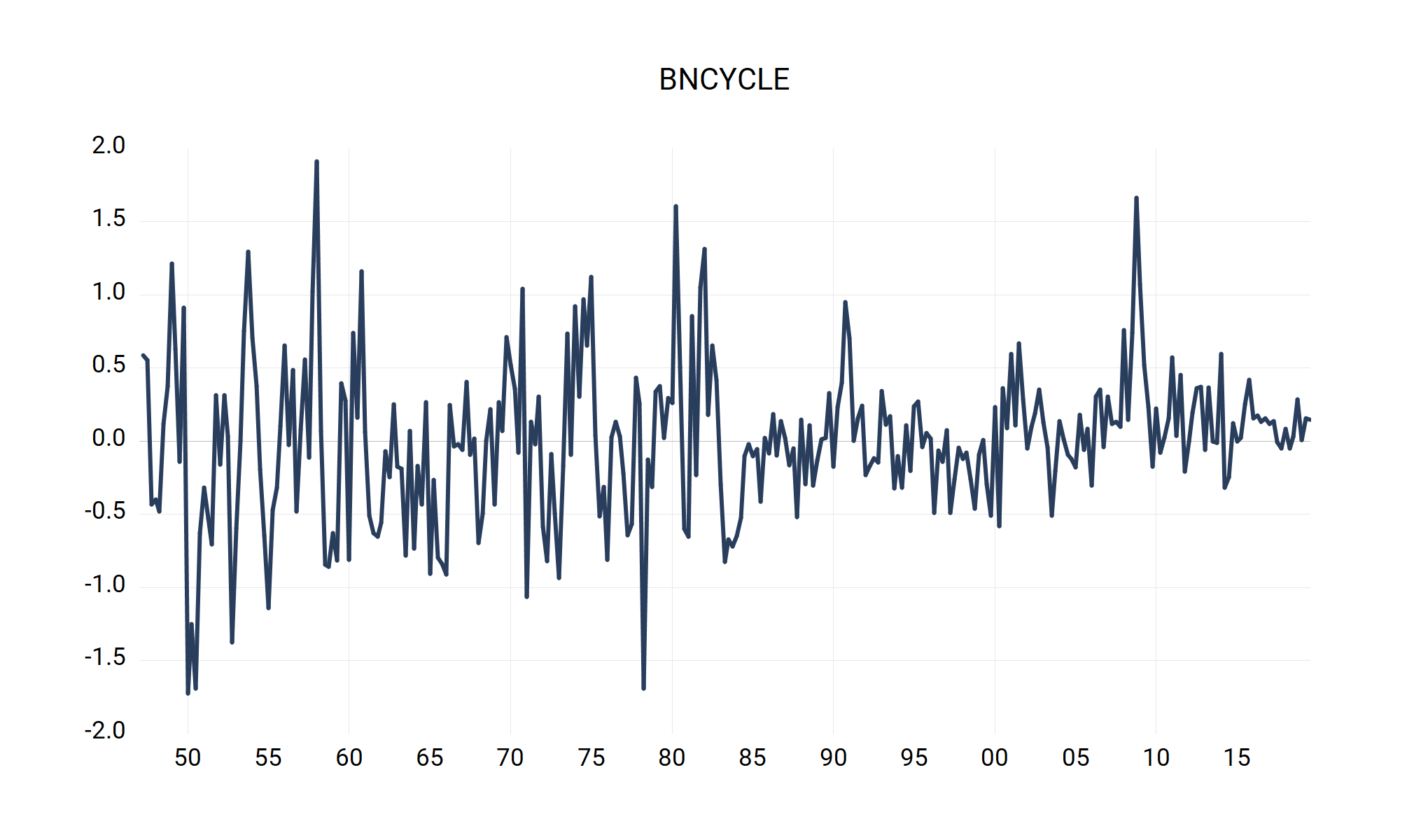 |
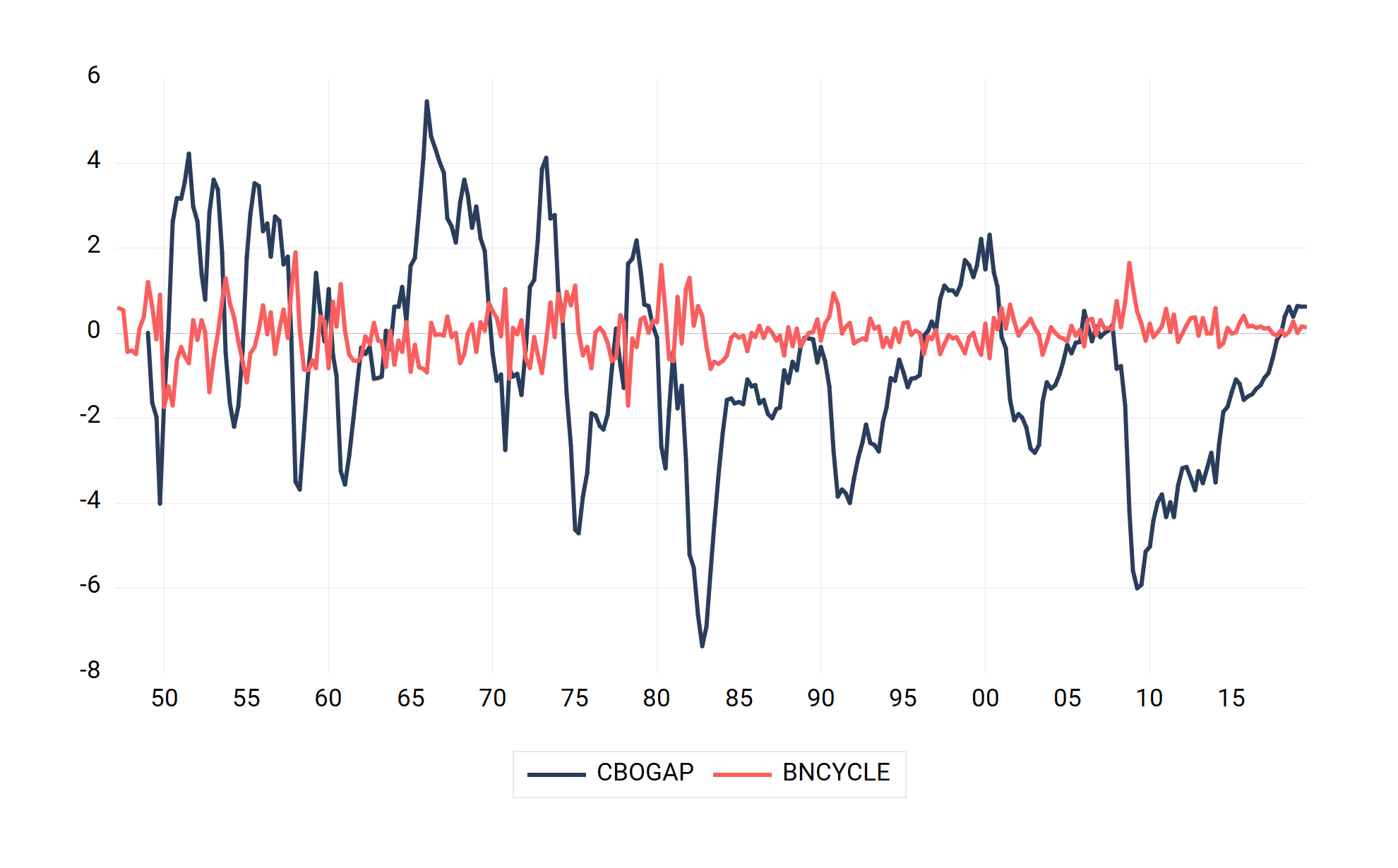 |
The BN Filter
First, to explain why the BN estimate of output gap lacks the persistence of its true counterpart, recall the formula for the BN cycle component for an AR(1) model: $$ c_{t} = y_{t} - \tau_{t} = -\frac{\phi}{1-\phi}(\Delta y_{t} - \mu)$$ Clearly, when $ \phi $ is small, $ \Delta y_{t} $ is not very persistent. Since $ c_{t} $ is only as persistent as $ \Delta y_{t} $, the cycle component itself lacks the persistence one expects of the true output gap series.Next, to explain why $ c_{t} $ lacks the expected amplitude, define the signal-to-noise ratio $ \delta $ for any time series as the ratio of the variance of trend shocks relative to the overall forecast error variance. In other words: $$ \delta \equiv \frac{\sigma^{2}_{\Delta \tau}}{\sigma^{2}_{\epsilon}} = \psi(1)^{2} $$ which follows since $ \Delta\tau = \psi(1)\epsilon_{t} $ and $ \psi(1) = \lim_{h\rightarrow \infty} \frac{\partial y_{t+h}}{\partial \epsilon_{t}} $. Intuitively, $ \psi(1) $ is the long-run multiplier that captures the permanent effect of the forecast error on the long-horizon conditional expectation of $ y_{t} $. Quite generally, as demonstrated in Kamber, Morley, and Wong (2018), for any AR(p) model: \begin{align} \Delta y_{t} = c + \sum_{k=1}^{p}\phi_{k}\Delta y_{t-k} + \epsilon_{t} \label{eq1} \end{align} the signal-to-noise ratio is given by the relation \begin{align} \delta = \frac{1}{(1-\phi(1))^{2}} \quad \text{where} \quad \phi(1) = \phi_{1} + \ldots + \phi_{p}\label{eq2} \end{align} In particular, when the forecasting model is AR(1), as was the case in the BN decomposition above, the signal-to-noise ratio is simply $ \delta = \frac{1}{(1-\phi)^{2}} $ and in the case of the US GDP growth process, it is $ \delta = \frac{1}{(1-0.36)^{2}} = 2.44$. In other words, the BN trend shocks exhibit higher volatility than quarter-to-quarter forecast errors and the signal-to-noise ratio is therefore relatively high. In fact, in the case of a stationary AR(1) model, the condition $ |\phi| < 1 $ implies that $ \delta> 0.25 $. In other words, trend shocks must explain at least 25% of the quarterly forecast error variance - evidently a strong assumption if one expects the cycle shocks (the output gap amplitude) to explain the majority of the systematic forecast variance.
To correct for the aforementioned shortcomings of the BN decomposition, Kamber, Morley, and Wong (2018) exploit the relationship between the signal-to-noise ratio and the AR coefficients in equation \eqref{eq2}. In particular, they note that equation \eqref{eq2} implies that: \begin{align} \phi(1) = 1 - \frac{1}{\sqrt{\delta}} \end{align} In this regard, the idea underlying the BN filter is to fix a specific value to the signal-to-noise ratio, say $ \delta = \bar{\delta} $. Subsequently, the BN decomposition is derived from an AR model, the AR coefficients of which are forced to sum to $ \bar{\phi}(1) \equiv 1 - \frac{1}{\sqrt{\bar{\delta}}} $. In other words, the BN decomposition is derived while imposing a particular signal-to-noise ratio.
It is important to note here that estimation of the BN decomposition under a particular signal-to-noise ratio restriction is in fact straightforward and does not require complicated non-linear routines. To see this, observe that equation \eqref{eq1} can be rewritten as: \begin{align} \Delta y_{t} = c + \rho \Delta y_{t-1} + \sum_{k=1}^{p-1}\phi^{\star}_{k}\Delta^{2} y_{t-k} + \epsilon_{t} \label{eq3} \end{align} where $ \rho = \phi_{1} + \ldots + \phi_{p} $ and $ \phi^{\star}_{k} = -\left(\phi_{k+1} + \ldots + \phi_{p}\right) $. Then, imposing the restriction $ \rho = \bar{\rho} \equiv \bar{\phi}(1) $ reduces the regresion in \eqref{eq3} to: \begin{align} \Delta y_{t} - \bar{\rho} \Delta y_{t-1} = c + \sum_{k=1}^{p-1}\phi^{\star}_{k}\Delta^{2} y_{t-k} + \epsilon_{t} \label{eq4} \end{align} In other words, $ \bar{\rho}\Delta y_{t-1} $ is brought to the left hand side and the regressand in the regression \eqref{eq4} becomes $ \Delta \bar{y}_{t} \equiv \Delta y_{t} - \bar{\rho} \Delta y_{t-1} $.
Why Use the BN Filter?
Before we demonstrate the BN Filter add-in, we quickly outline two reasons why the BN filter might be a reasonable approach, particularly when estimating the output gap.- When analyzing GDP growth, standard ARMA model selection often favours low order AR variants, which, as discussed earlier, produce high signal-to-noise ratios.
- Unlike alternative low signal-to-noise ratio procedures such as deterministic quadratic detrending, the Hodrick-Prescott (HP) filter, and the bandpass (BP) filter, which often require large number of estimation revisions (as new data comes in) and are typically unreliable in out-of-sample forecasts (see Orphanides and Van Norden, (2003)), Kamber, Morley and Wong (2018) argue that the BN filter exhibits better out-of-sample performance and generally requires fewer estimation revisions to match observable data characteristics.
To estimate the HP filter cycle component for the period 1947Q1 to 2008Q3, we first set the sample accordingly by issuing the command:
Next, we estimate the HP filter cycle series as follows:
smpl @first 2008Q3
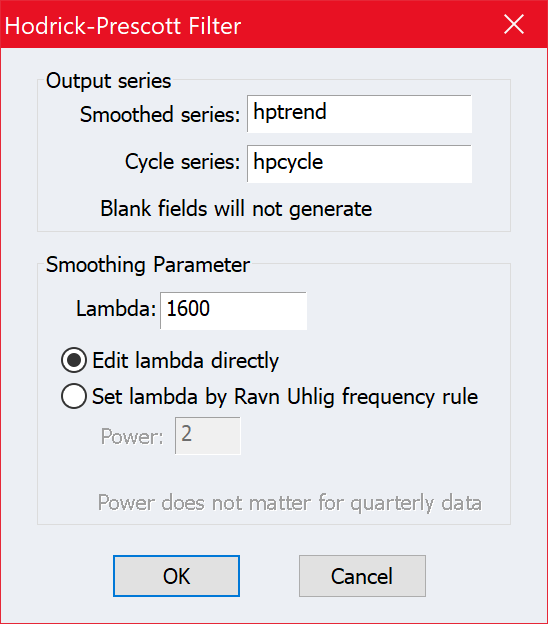
- From the workfile, double click on the series LOGGDP to open the series.
- In the series window, click on Proc/Hodrick-Prescott Filter...
- In the Cylce series text box, type hpcycle.
- Hit OK.
 |
 |
BN Filter Implementation
To implement the BN Filter, we need to download and install the add-in from the EViews website. The latter can be found at https://www.eviews.com/Addins/BNFilter.aipz. We can also do this from inside EViews itself:- From the main EViews window, click on Add-ins/Download Add-ins...
- Click on the the BNFilter add-in.
- Click on Install.
 |
- From the workfile window, double click on LOGGDP to open the spreadsheet view of the series.
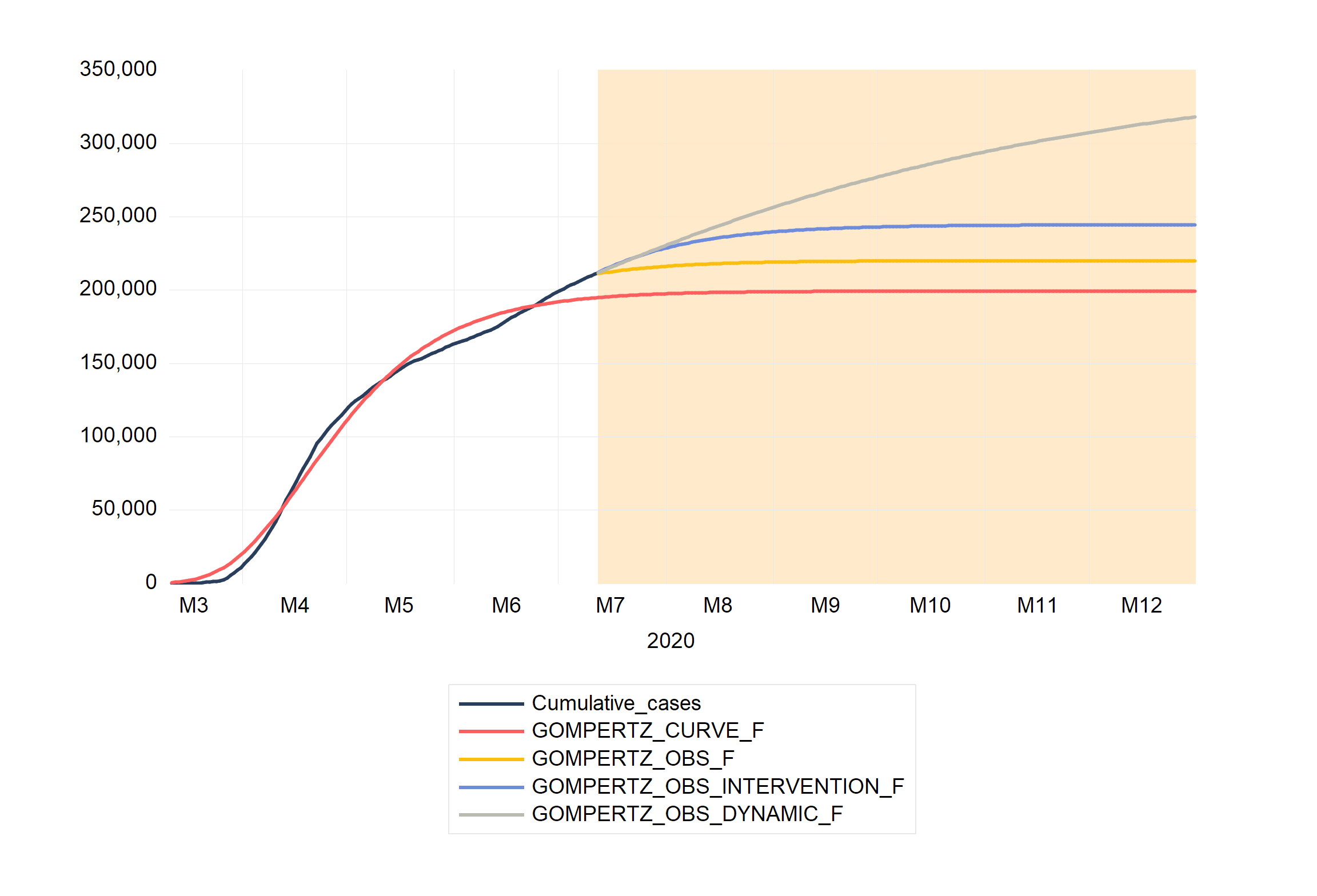
- To access the BN filter dialog, click on Proc/Add-ins/BN Filter
- Stick with the defaults and hit OK.
 |
 |  |
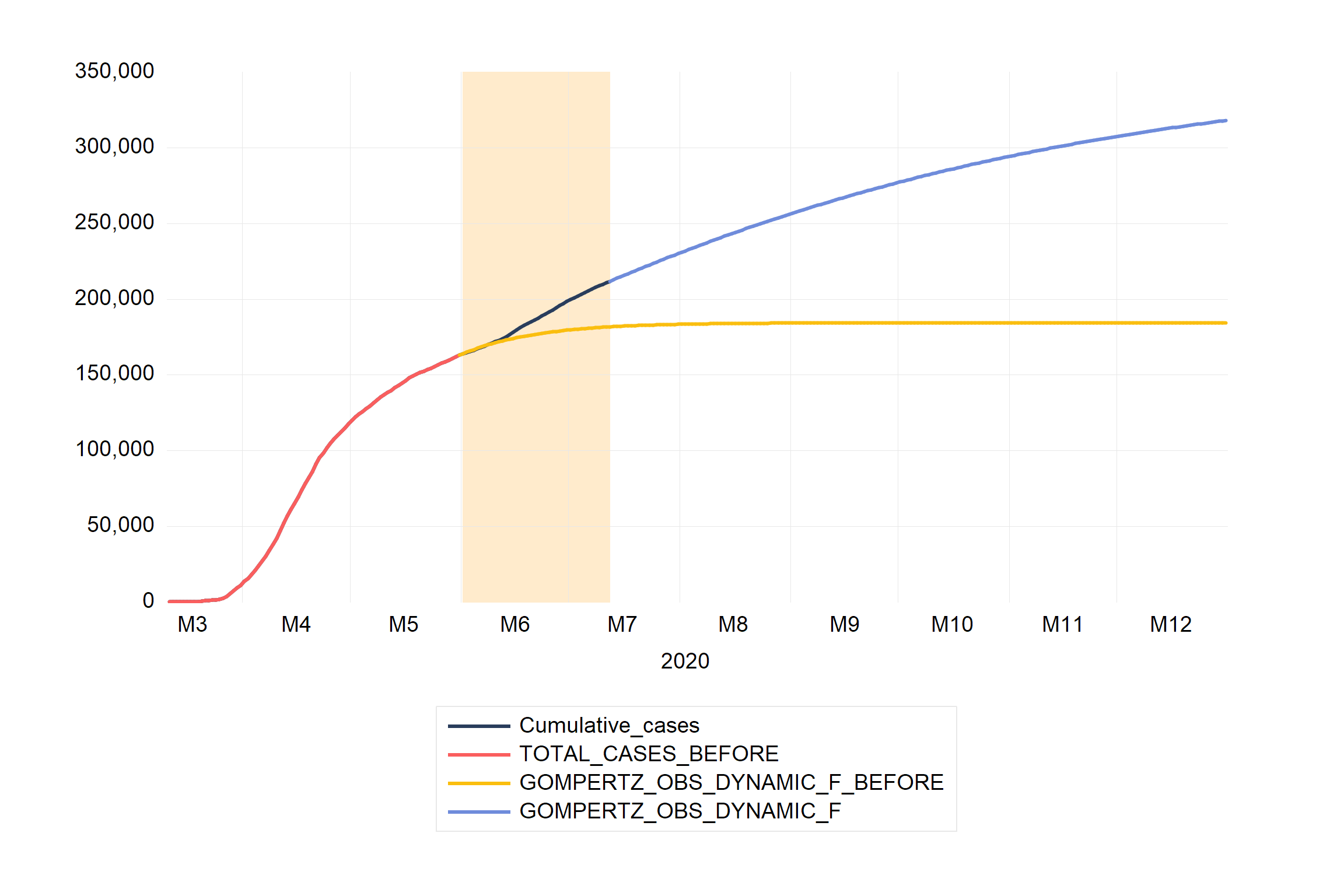
The BN filter add-in also accommodates the ability to incorporate knowledge about structural breaks. In particular, we will use 2006Q1 as a structural break which is consistent with the date found by a Bai and Perron (2003) test, used by Kamber, Morley and Wong (2018), and is consistent with independent work by Eo and Morley (2019). The following steps demonstrate the outcome:
- From the workfile window, double click on LOGGDP to open the spreadsheet view of the series.
- To access the BN filter dialog, click on Proc/Add-ins/BN Filter
- Select the Structural Break box.
- In the Date of structural break text box, enter 2006Q1.
- Hit OK.
 |
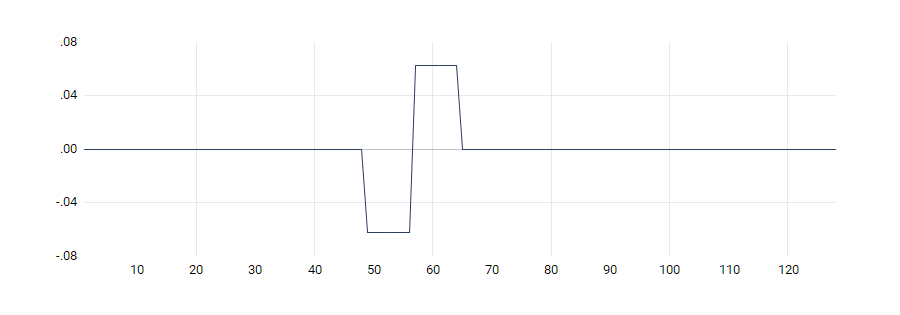
Suppose however that we were ignorant about the actual date of the break. This might be the case in practice as it could take a decade or more before one could empirically identify a structural break date. In this case, a possible option is to use a rolling window for the average growth rate. In this example, we use a backward window of 40 quarters as the average growth rate. The idea is that if there were breaks, they would be reflected in this window. When this is the case, we proceed as follows:
- From the workfile window, double click on LOGGDP to open the spreadsheet view of the series.
- To access the BN filter dialog, click on Proc/Add-ins/BN Filter
- Select the Dynamic mean adjustment box.
- Hit OK.
 | 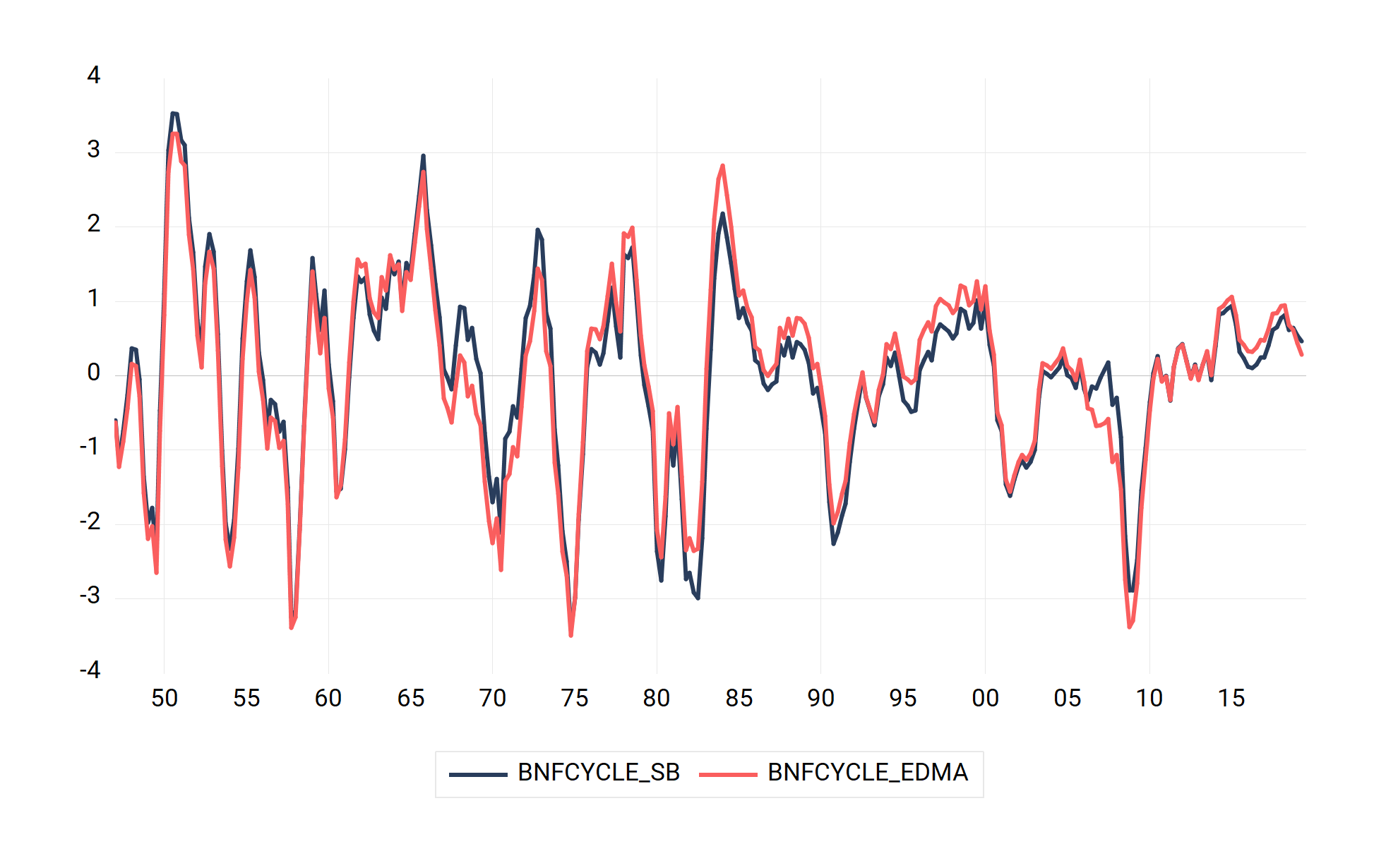 |
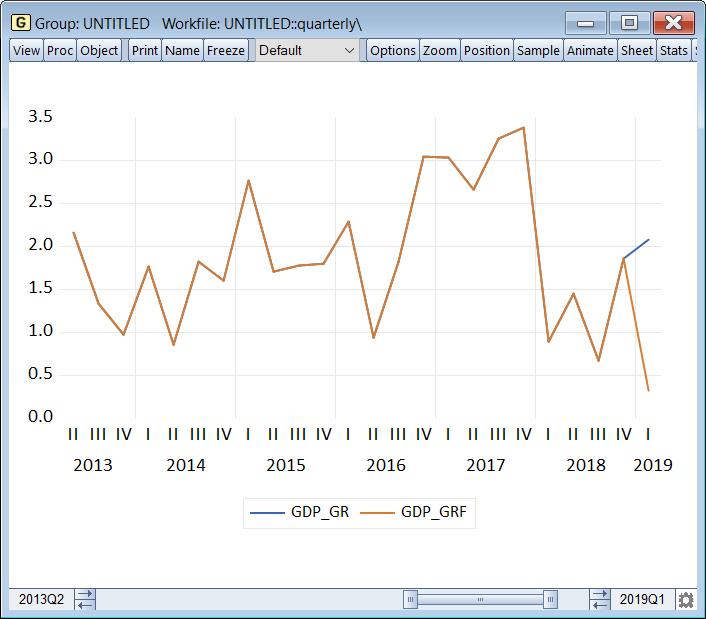
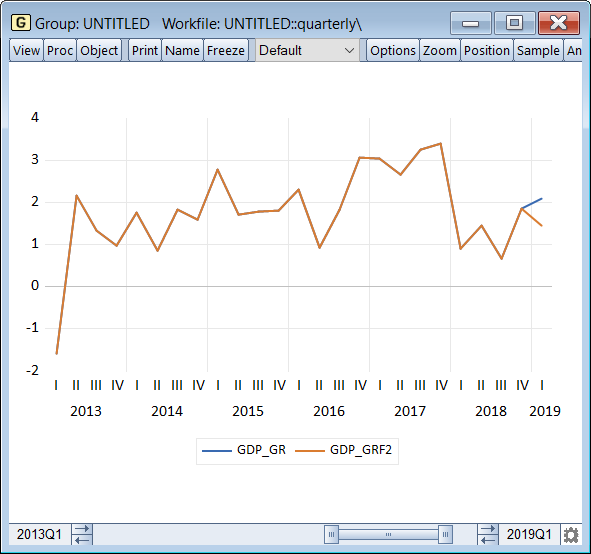
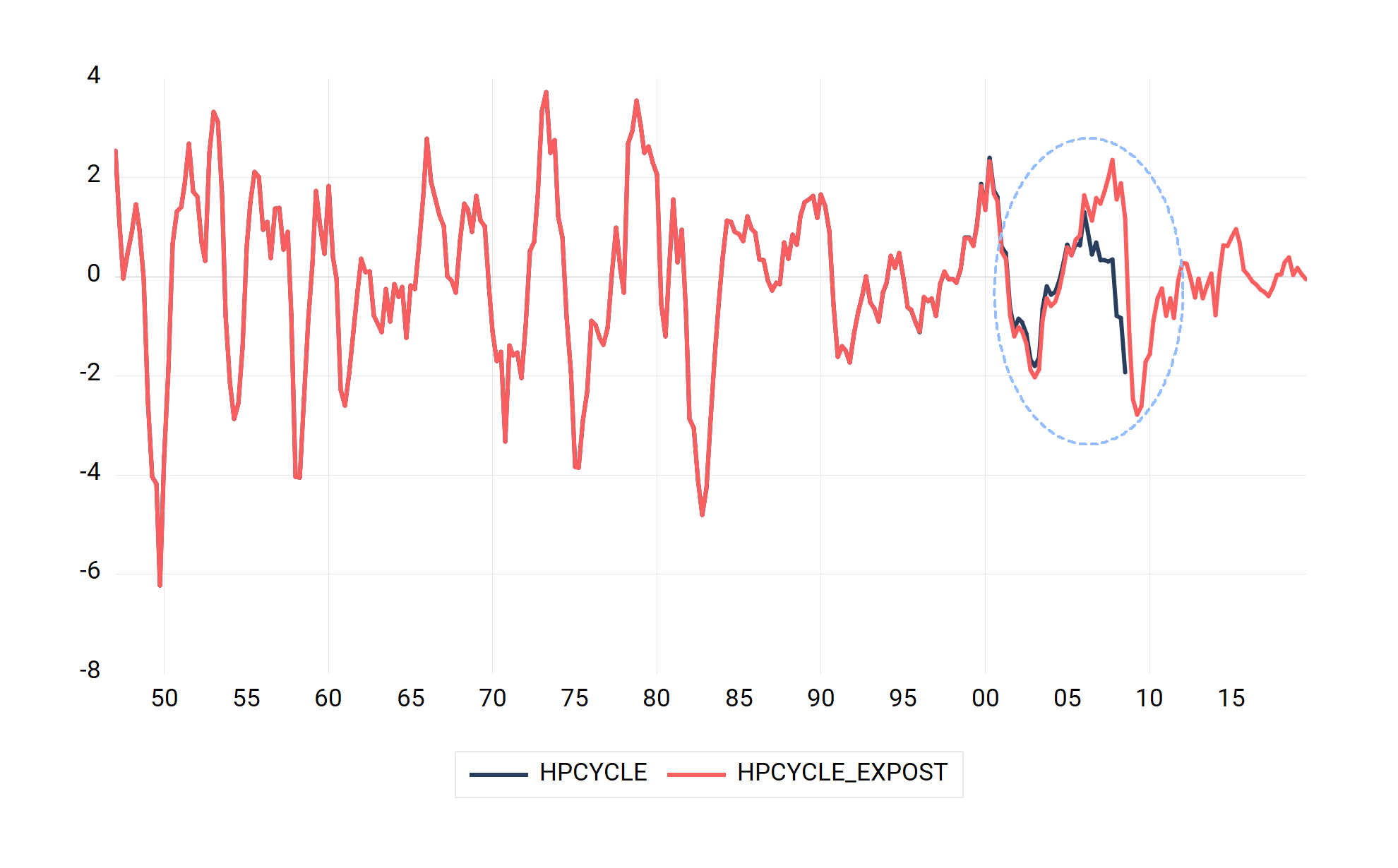
Finally, we come back to the issue of revision. As we mentioned earlier, the BN filter should produce output gaps that are less revised as long as the AR forecasting model is stable, especially when compared to the heavily revised HP Filter. Here, we show the output gap estimated using the BN filter with data up to 2008Q3, and one ex-post up to 2019Q3. Clearly, the output gap is hardly revised, which address a key critique of Orphanides and Van Norden (2003).
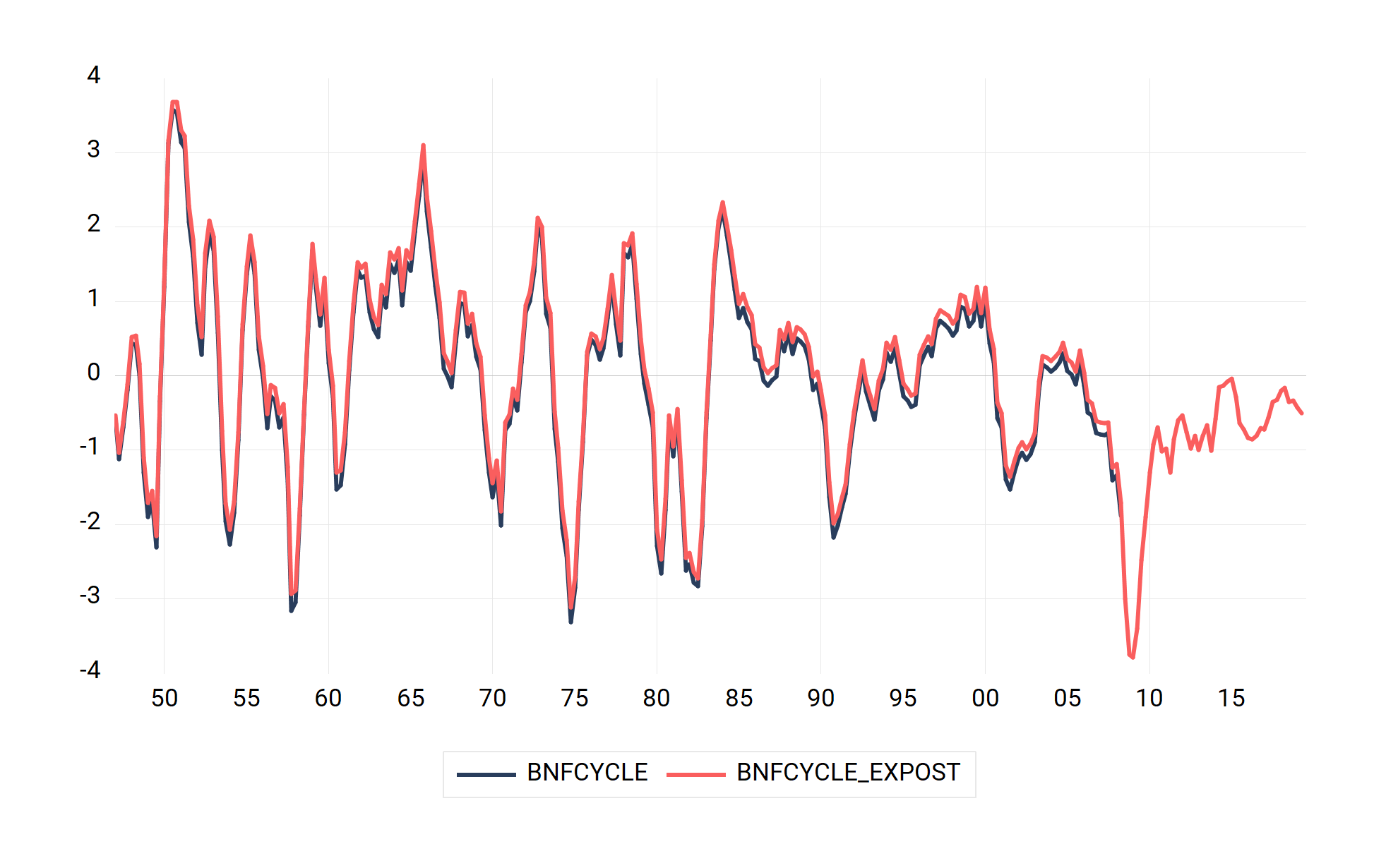 |
Conclusion
In this blog post we have outlined the BN filter add-in associated with the work of Kamber, Morley and Wong (2018). In general, we hope the ease of using the add-in, together with some of the useful properties of the BN Filter will encourage practitioners to explore using the procedure in their work.Files
References
- Bai J. and Perron P.: Computation and analysis of multiple structural change models Journal of Applied Econometrics, 18(1) 1–22, 2003.
- Beveridge S. and Nelson C. R.: A new approach to decomposition of economic time series into permanent and transitory components with particular attention to measurement of the business cycle Journal of Monetary Economics, 7(2) 151–174, 1981.
- Eo Y. and Morley J.: Why has the US economy stagnated since the Great Recession University of Sydeny Working Papers 2017-14, 2019.
- Kamber G., Morley J., and Wong B.: Intuitive and reliable estimates of the output gap from a Beveridge-Nelson filter The Review of Economics and Statistics, 100(3) 550–566, 2018.
- Orphanides A and Van Norden S.: The unreliability of output-gap estimates in real time The Review of Economics and Statistics, 84(4) 569–583, 2002.
- Watson M.: Univariate detrending methods with stochastic trends Journal of Monetary Economics, 18(1) 49–75, 1986.